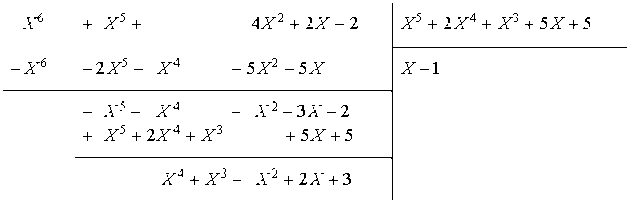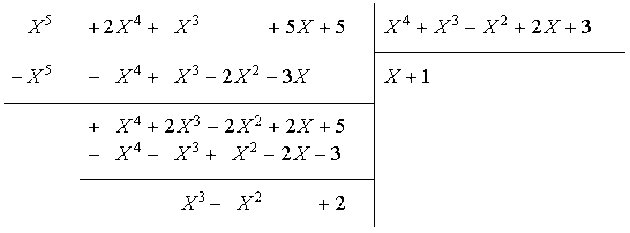PGCD et recherche d'un couple vérifiant l'identité de Bézout
Partie
Question
Trouver le PGCD, noté \(D\), dans \(K[X]\)(\(K\) étant \(R\) ou \(C\)), des polynômes \(A\) et \(B\) suivants :
\(A(X)=X^6+X^5+4X^2+2X-2\)
\(B(X)=X^5+2X^4+X^3+5X+5\)
et déterminer un couple \((U,V)\) de polynômes vérifiant l'identité de Bézout \(AU+BV=D\).
Aide simple
On effectue des divisions euclidiennes successives et le PGCD est le dernier reste non nul à une constante multiplicative près.
Dans l'algorithme de détermination d'un couple \((U,V)\) vérifiant l'identité \(AU+BV=D\) où \(D\) est le PGCD de \(A\) et \(B\), on donne, dans chaque division euclidienne, l'expression du reste en fonction d'abord des polynômes ' dividende ' et ' diviseur ' pour pouvoir les écrire ensuite en fonction des deux polynômes dont on cherche le PGCD.
Aide méthodologique
Mettre en œuvre les algorithmes de recherche du PGCD de deux polynômes et des couples intervenant dans l'identité de Bézout.
Solution détaillée
On recherche le PGCD des polynômes \(A\) et \(B\) par l'algorithme d'Euclide, utilisant les divisions euclidiennes des polynômes : le PGCD est alors le dernier reste non nul à une constante multiplicative près (le PGCD est un polynôme unitaire).
On obtient \(A=q_1B+r_1\), avec \(q_1(X)=X-1\)et \(r_1=X^4+X^3-X^2+2X+3\).
On fait ensuite la division euclidienne de \(B\) par \(r_1\):
On obtient \(B=q_2r_1+r_2\), avec \(q_2(X)=X+1\) et \(r_2(X)=X^3-X^2+2\).
On fait la division euclidienne de \(r_1\) par \(r_2\):
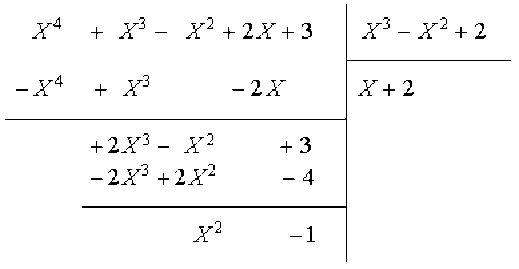
On obtient \(r_1=q_3r_2+r_3\), avec \(q_3(X)=X+2\) et \(r_3(X)=X^2-1\).
On fait la division euclidienne de \(r_2\) par \(r_3\):
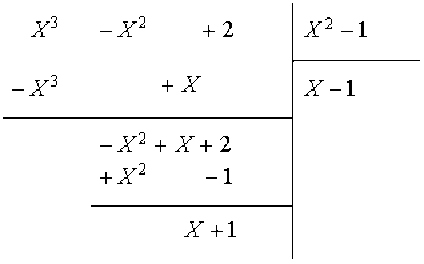
On obtient \(r_2=q_4r_3+r_4\), avec \(q_4(X)=X-1\) et \(r_4(X)=X+1\).
Il est immédiat que \(r_3(X)=(X-1)r_4(X)\).
Donc \(r_4\) est le dernier reste non nul, c'est donc le PGCD de \(A\) et \(B\).
\(r_4(X)=PGCD(A(X),B(X))\)
\(PGCD(A(X),B(X))=X+1\)
On regroupe les résultats obtenus pour se servir de l'algorithme de détermination des polynômes \(U\) et \(V\) tels que \(PGCD(A,B)=AU+BV\):
\(A=q_1B+r_1\), avec \(q_1(X)=X-1\)
\(B=q_2r_1+r_2\), avec \(q_2(X)=X+1\)
\(r_1=q_3r_2+r_3\), avec \(q_3(X)=X+2\)
\(r_2=q_4r_3+r_4\), avec \(q_4(X)=X-1\)
D'où :
Donc on a déterminé un couple \((U,V)\) de polynômes vérifiant l'égalité \(PGCD(A,B)=AU+BV\),
en posant \(U(X)=-X^3-2X^2-X+2\) et \(V(X)=X^4+X^3-2X+1\),
le couple \((U(X),V(X))\)vérifie bien :
\(PGCD(A(X),B(X))=U(X)A(X)+V(X)B(X)\)