Symétrie
Soit \(E\) un espace vectoriel de type fini.
Définition :
Soient \(F\) et \(G\) deux sous-espaces vectoriels de \(E\), non réduits au vecteur nul et supplémentaires, donc tels que \(E=F\oplus G\) . Pour tout \(x\) de \(E\), il existe un unique couple \((y,z)\) appartenant à \(F\times G\) tel que . L'application :
\(\begin{array}{cccccc}s :E&=&F\oplus G&\to&E\\x&=&y+z&\mapsto&y-z\end{array}\)
est la symétrie par rapport au sous-espace \(F\) parallèlement à \(G\).
Symétrie dans \(\mathbb R^2\)
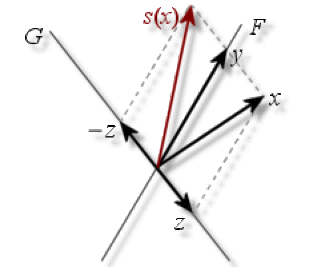
Symétrie dans \(\mathbb R^3\)
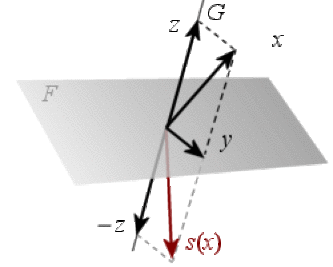
On a immédiatement les propriétés suivantes :
Proposition : Propriétés vectorielles
Une symétrie est une application linéaire.
Si \(s\) est la symétrie par rapport au sous-espace vectoriel \(F\) parallélement à \(G\), alors les sous espaces vectoriels \(F\) et \(G\) sont stables par \(s\). La restriction de \(s\) à \(F\) est l'identité ; la restriction de \(s\) à \(G\) est l'homothétie de rapport \(-1\) . On a :
\(\begin{array}{cccccc}\forall x&\in&F,s(x)&=&x\\\forall x&\in&G,s(x)&=&-x\end{array}\)
Théorème : Caractérisation d'une symétrie
Si \(s\) est une symétrie, on a : \(s^2=Id_E\)
Réciproquement si \(s\) est un endomorphisme de \(E\) tel que \(s^2=Id_E\), alors \(s\) est la symétrie par rapport à \(F=\{x\in E,s(x)=x\}\) parallèlement à \(G=\{x\in E,s(x)=-x\}\).
Remarque :
un endomorphisme \(f\) qui vérifie une relation de la forme \(f^2=Id_E\) est une involution.
Preuve :
preuve de la propriété 1 :
La propriété 1. est immédiate d'après la définition de \(s\).
preuve de la propriété 2 : (deux méthodes)
première méthode :
La première étape de la preuve de la propriété 2. consiste à démontrer que \(F\) et \(G\) définis par \(F=\{x\in E,s(x)=x\}\) et \(G=\{x\in E,s(x)=-x\}\) sont des sous-espaces vectoriels supplémentaires.
Ce sont des sous-espaces vectoriels car ce sont des noyaux d'endomorphismes : \(F=\textrm{ ker }(s-Id_E)\) et \(G=\textrm{ ker }(s-Id_E)\).
Ils sont supplémentaires. En effet, soit \(x\) un élément de \(F\cap G\). Il vérifie les deux relations \(s(x)=x\) et \(s(x)=-x\). D'où l'égalité \(2x=0\). Le vecteur \(x\) est donc le vecteur nul.
Soit \(t\) un élément quelconque de \(E\). Considérons les éléments \(\displaystyle{y=\frac{t+s(t)}{2}}\) et \(\displaystyle{z=\frac{t-s(t)}{2}}\). Il est facile de vérifier que \(y\) est élément de \(F, z\) élément de \(G\) et que \(t=y+z\) . Donc \(E=F\oplus G\).
Pour conclure, il suffit de vérifier que \(s(t)=y-z\) ce qui est immédiat.
On peut aussi faire une démonstration plus élégante, utilisant la notion de polynôme minimal.
Soit donc \(s\) est un endomorphisme de \(E\) tel que \(s^2=Id_E\). Le polynôme \(X^2-1\) est un polynôme annulateur de \(s\). Le polynôme minimal de \(s\) divise donc \(X^2-1\) et par conséquent n'a que des racines simples. L'endomorphisme \(s\) est donc diagonalisable. Trois cas sont possibles :
Ou bien \(s=Id_E\), alors \(F=E\) et \(G=\{0\}\).
Ou bien \(s=-Id_E\) alors \(F\{0\}\) et \(G=E\).
Ou bien \(s\neq Id_E\) et \(s\neq-Id_E\), alors les valeurs propres de \(s\) sont \(1\) et \(-1\), \(F\) est le sous-espace propre associé à la valeur propre \(1,G\) est le sous-espace propre associé à la valeur propre \(-1\) et \(E=F\oplus G\), puisque \(s\) est diagonalisable.
Dans les trois cas, la propriété est vraie.
La propriété pour une symétrie d'être diagonalisable est démontrée par des moyens élémentaires dans la propriété suivante.
Enfin on a le résultat suivant sur la matrice associée à une symétrie dans une base bien choisie.
Proposition : Matrice associée à une symétrie
Soient \(F\) et \(G\) deux sous-espaces vectoriels de \(E\) supplémentaires, non réduits au vecteur nul \((E=F\oplus G)\). Soient \(B_F\) et \(B_G\) des bases de \(F\) et \(G\) respectivement. Soit \(s\) la symétrie par rapport au sous-espace \(F\) parallèlement à \(G\). Sa matrice dans la base déterminée par la réunion des vecteurs de \(B_F\) et \(B_G\) est égale à \(\left(\begin{array}{cc}I_r&0\\0&-I_q\end{array}\right)\) où \(r\) est la dimension de \(F\) et \(q\) celle de \(G\).
On peut interpréter ce résultat dans le langage de la théorie de la diagonalisation. En effet ce résultat signifie que la symétrie par rapport à \(F\) parallèlement à \(G\) est diagonalisable, que ses valeurs propres sont \(1\) et \(-1\) et enfin que le sous espace propre associé à la valeur propre \(-1\) est \(G\) et celui associé à la valeur propre \(1\) est \(F\).
Remarque :
Relation entre symétrie et projecteur
Soient \(F\) et \(G\) deux sous-espaces vectoriels de \(E\), non réduits au vecteur nul et supplémentaires. Il est facile de vérifier la relation : \(s=2p-Id_E\) , avec \(s\) symétrie par rapport au sous-espace \(F\) parallèlement à \(G\) et \(p\) est la projection sur le sous-espace \(F\) parallèlement à \(G\).
Comme pour les projecteurs, cela donne un exemple d'endomorphisme diagonalisable ayant un nombre de valeurs propres distinctes strictement inférieur à la dimension \(n\) de l'espace considéré (sauf dans le cas où \(n=2\)).