Théorème des séries alternées
Théorème :
On considère une série dont le terme général s'écrit, pour tout entier \(n\), sous la forme \(u_n=(-1)^nv_n\) avec \(v_n\geq 0\). On suppose réalisées les conditions suivantes :
(i) la suite \((v_n)\) est décroissante,
(ii)\(\displaystyle{\lim_{n\rightarrow+\infty}}v_n=0\)
Alors la série de terme général \(u_n\) est convergente.
Bien évidemment le théorème s'applique, dans les mêmes conditions, pour une série dont le terme général s'écrit \(u_n=(-1)^{n+1}v_n\) avec \(v_n\geq 0\). Le théorème qui concerne la majoration du reste et l'encadrement de la somme est énoncé pour le cas d'une série de terme général \(u_n=(-1)^nv_n\) avec \(v_n\geq 0\), le passage à l'autre cas étant immédiat.
Preuve :
Méthode : on montre que les suites des sommes partielles \((s_{2p})\) et \((s_{2p+1})\) sont adjacentes.
La décroissance de la suite \((v_n)\) entraîne les inégalités :
\(s_{2p+2}-s_{2p}=v_{2p+2}-v_{2p+1}\leq 0\) et \(s_{2p+1}-s_{2p-1}=v_{2p}-v_{2p+1}\geq 0\).
La suite \((s_{2p})\) est décroissante et la suite \((s_{2p+1})\) est croissante. On a également, pour tout entier \(p\) :
\(s_{2p+1}-s_{2p}=-v_{2p+1}\leq 0\).
On en déduit, d'une part \(s_{2p+1}\leq s_{p2}\) et d'autre part \(\displaystyle{\lim_{p\rightarrow+\infty}}(s_{2p+1}-s_{2p})=0\).
Les suites \((s_{2p})\) et \((s_{2p+1})\) sont adjacentes. Elles sont donc convergentes, de même limite, et la suite \((s_n)\) est convergente.
Remarque :
On a : \(\forall n\in \mathbb N\), \(v_n=|u_n|\). On énonce parfois le critère en rassemblant les deux conditions (i) et (ii) sous la forme abrégée : la valeur absolue du terme général tend vers 0 en décroissant.
Théorème : Majoration du reste d'une série satisfaisant aux hypothèses du théorème des séries alternées.
Soit \(\sum u_n\) une série qui satisfait aux hypothèses du théorème des séries alternées. Alors, pour tout entier \(n\), le reste d'ordre \(n\), \(r_n\), vérifie les propriétés suivantes :
\(r_n\) est du signe de \(u_{n+1}\);
\(|r_n|\leq|u_{n+1}|\).
Preuve :
C'est une conséquence du theoréme précédent.
D'après la démonstration précédente, on a, pour tout entier \(p\) : \(s_{2p+1}\leq s\leq s_{2p}\), d'où
\(r_{2p}=s-s_{2p}\leq 0\) et \(r_{2p+1}=s-s_{2p+1}\geq 0\).
On en déduit : \(|r_{2p}|=s_{2p}-s\leq s_{2p}-s_{2p+1}=v_{2p+1}\) et \(r_{2p+1}=s-s_{2p+1}\leq s_{2p+2}-s_{2p+1}=v_{2p+2}\).
Remarque :
Le théorème des séries alternées permet de montrer que des séries comme les séries de terme général \(\frac{(-1)^n}{n},\frac{(-1)^n}{\sqrt{n}},(-1)^n\sin{\frac{1}{n}}(n\geq 1)\) et \(\frac{(-1)^n}{\ln n}(n\geq 2)\), qui ne sont pas absolument convergentes, sont convergentes.
Mais il faut insister sur le fait que, pour des séries comme les séries de terme général \(\left(\frac{(-1)^n}{n^s}\right)\), avec \(s>1\), qui sont absolument convergentes, on n'utilise pas le théorème des séries alternées pour les étudier. Celui-ci ne permet de conclure qu'à la convergence de la série et non l'absolue convergence.
Rappelons que, pour une série à termes qui ne sont pas tous de même signe, on commence toujours par étudier la série des valeurs absolues.
En revanche, pour une telle série, on peut utiliser la majoration du reste déduite du théorème des séries alternées.
L'hypothèse concernant la décroissance de la suite \(v_n\) est indispensable pour appliquer le théorème.
Considérons, par exemple, la série de terme général \(u_n=\frac{(-1)^n}{\ln n+(-1)^n}(n\geq 1)\). Le terme général s'écrit : \(u_n=(-1)^nv_n\) avec \(v_n>0\) et \(\displaystyle{\lim_{n\rightarrow+\infty}}v_n=0\), mais la suite \((v_n)\) n'est pas décroissante.
On a :
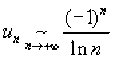. On pose : \(\forall n\geq 2\), \(w_n=\frac{(-1)^n}{\ln n}-u_n=\frac{1}{\ln^2n+(-1)^n\ln n}\).La série de terme général \(w_n\) est à termes positifs et
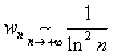. Comme \(nw_n\) tend vers \(+\infty\) quand \(n\) tend vers l'infini, la série de terme général \(w_n\) est donc divergente (cf. les séries de Bertrand). La série \(\sum u_n\) est la différence d'une série convergente \(\displaystyle{\sum_{n\geq 2}}\frac{(-1)^n}{\ln n}\) et d'une série divergente \(\displaystyle{\sum_{n\geq 2}}w_n\). Elle est donc divergente.Cet exemple présente aussi l'intérêt de mettre en évidence deux séries, l'une convergente, l'autre divergente, dont les termes généraux sont équivalents. Il montre que le théorème de comparaison ne s'applique qu'à des séries à termes tous de même signe.