Le courant électrique

On peut, statistiquement, définir un modèle macroscopique décrivant les phénomènes microscopiques. Dans ce modèle, tous les porteurs de charge se déplacent à la vitesse moyenne v appelée vitesse d'entraînement ou vitesse de dérive.

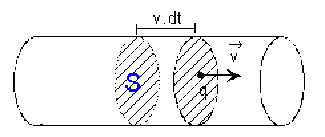
Considérons un conducteur en régime permanent. Soient :

• n le nombre de porteurs mobiles par unité de volume du conducteur (en \(\textrm{m}^{-3}\))

• q la charge de chaque porteur

• S la surface d'une section droite du conducteur (en \(\textrm{m}^2\))

• v la vitesse moyenne d'entraînement des porteurs de charge (en \(\textrm{m.s}^{-1}\))

Un porteur de charge traversera la section pendant la durée élémentaire \(\textrm{d}t\) si la distance qu'il doit parcourir est inférieure à \(v.\textrm{d}t\). La quantité d'électricité qui traverse une section du conducteur pendant la durée élémentaire \(\textrm{d}t\) correspond donc à la charge des porteurs se trouvant dans le volume \(S.v.\textrm{d}t\).

\(\textrm{d}q = n.q.S.v.\textrm{d}t\)

D'où l'intensité du courant traversant le conducteur :

\(I=\frac{\textrm{d}q}{\textrm{d}t}=n.q.S.v\)