Association en parallèle : Définition
Association en parallèle : Définition
Définition :
Des dipôles[1] sont associés en parallèle[2] s'ils ont les mêmes bornes. Ils sont alors soumis à la même différence de potentiel[3], mais sont parcourus par des courants différents, puisque les charges mobiles vont se répartir entre les différentes branches. Comme il ne peut pas y avoir accumulation de charges, la somme des charges qui arrivent est égale à la somme des charges qui traversent les trois branches. L' intensité[4] dans le circuit principal est égale à la somme des intensités dans les trois branches :
\(I = I_1 + I_2 + I_3\)
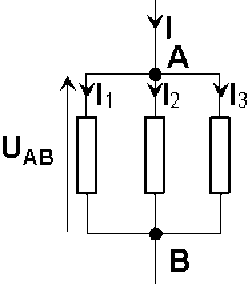
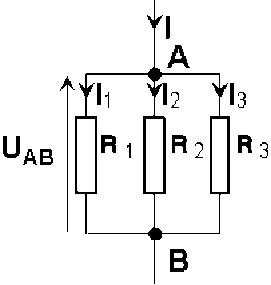
Association en parallèle - Association de conducteurs ohmiques en parallèle
Aux bornes de chaque élément la loi d'Ohm est vérifiée :
\((V_A - V_B) = R_1.I_1 = R_2.I_2 = R_3.I_3\)
\(I = I_1 + I_2 + I_3\)
\(I=\frac{V_A-V_B}{R_1}+\frac{V_A-V_B}{R_2}+\frac{V_A-V_B}{R_3}\)
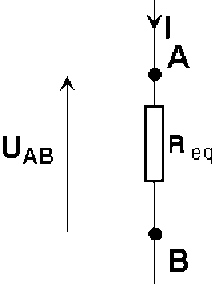
Un dipôle[1] sera équivalent à l'association si, placé entre A et B et soumis à la même différence de potentiel[3], il est parcouru par un courant ayant la même intensité[4] I :
\(I=\frac{V_A-V_B}{R_\textrm{eq}}\)
donc : \(\frac{V_A-V_B}{R_\textrm{eq}}=\frac{V_A-V_B}{R_1}+\frac{V_A-V_B}{R_2}+\frac{V_A-V_B}{R_3}\)
d'où : \(\frac{1}{R_\textrm{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\)
si on utilise les conductances[5] des dipôles ( \(G = 1/R\) ), on obtient :
\(G_\textrm{eq} = G_1 + G_2 + G_3\)
Association en parallèle :
Dans une association en parallèle de conducteurs ohmiques, l'ensemble est équivalent à un dipôle unique dont la conductance est la somme des conductances :
\(G_\textrm{eq}=\displaystyle{\sum_i}G_i\)
L'unité de conductance est le Siemens (S). Par exemple, un dipôle dont la résistance[6] vaut 1 k \(\Omega\) a une conductance de 1 mS. Mais de nombreux livres utilisent encore comme unité l'inverse de l'ohm (\(\Omega^{-1}\) ou mho).