Montages basés sur les lois d'association
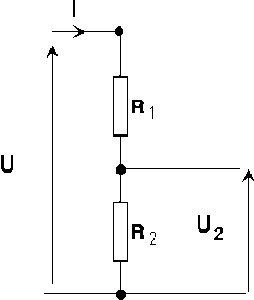
Montage diviseur de tension
Définition : Diviseur de tension
On appelle diviseur de tension[1] un montage dans lequel une tension[2] est appliquée aux bornes de deux dipôles[3], de résistances[4] \(R_1\) et \(R_2\), montés en série. Exprimons \(U_2\) en fonction de la tension U appliquée et des résistances :
\(U_2 = R_2.I\)
\(U = (R_1+R_2).I\)
d'où :
\(\frac{U_2}{U}=\frac{R_2}{R_1+R_2}\)
Le rapport des tensions est égal au rapport des résistances aux bornes desquelles on mesure ces tensions.
Fondamental : Diviseur de tension
\(U_2=\frac{R_2}{R_1+R_2}.U\)
La tension U2 n'est qu'une fraction de U, d'où le nom de diviseur de tension.
Cette formule toute simple est d'une grande importance et intervient souvent dans la résolution des problèmes. Mais attention : le diviseur est parfois dessiné de manière différente ! Il faut apprendre à le reconnaître.
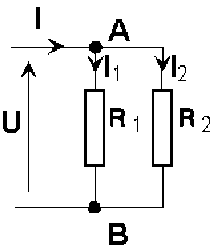
Montage diviseur de courant
Diviseur de courant
On appelle diviseur de courant[5] un montage (ou une partie de montage) dans lequel un courant d' intensité[8] I est injecté aux bornes de deux dipôles[3] , de résistances[4] \(R_1\) et \(R_2\), montés en parallèle[9]. Soit U la différence de potentiel[6] aux bornes communes des deux dipôles. Soit I2 l'intensité du courant traversant le dipôle de résistance R2. Exprimons I2 et I en fonction de U et des conductance[7] s :
\(I_2=G_2.U\)
\(I = ( G_1 + G_2 ) . U\)
\(\frac{I_2}{I}=\frac{G_2}{G_1+G_2}\)
Le rapport des intensités dans les branches est égal au rapport des conductances correspondantes.
Le courant I2 n'est qu'une fraction de I, d'où le nom de diviseur de courant.
Fondamental : Diviseur de courant
\(I_2=\frac{G_2}{G_1+G_2}.I\)
Cette formule toute simple est d'une grande importance et intervient souvent dans la résolution des problèmes. Mais attention : le diviseur est parfois dessiné de manière différente! Il faut apprendre à le reconnaître.