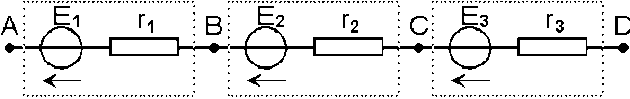Générateurs

De même que pour simplifier la résolution des problèmes, on a remplacé un réseau de conducteurs ohmiques par un dipôle équivalent unique, on va chercher à remplacer un ensemble de générateurs^[1] par un seul générateur, équivalent à l'ensemble.

Dans ce cas, il est souhaitable d'utiliser le modèle de Thévenin. A vide, aucun courant ne circule dans les trois dipôles^[2] et :

\((V_A -V_D) = (V_A - V_B) + (V_B - V_C) + (V_C - V_D)= E_1 + E_2 + E_3\)

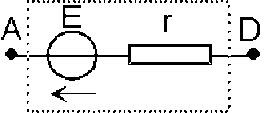
Pour le générateur^[1] équivalent, à vide :

\((V_A - V_D) = E\)

D'où :

\(E = E_1 + E_2 + E_3\)

Si on relie A et D par un court circuit, les trois dipôles sont parcourus par le même courant d' intensité \(I_0\) ; donc:

\((V_A -V_D) = (V_A - V_B) + (V_B - V_C) + (V_C - V_D)\)

\(0 = (E_1 - r_1.I_0) + (E_2 - r_2.I_0) + (E_3 - r_3.I_0)\)

\(0 = E_1 + E_2 + E_3 -( r_1+r_2+r_3) I_0\)

D'où:

\(I_0=\frac{E_1+E_2+E_3}{r_1+r_2+r_3}=\frac{E}{r_1+r_2+r_3}\)

Pour le générateur équivalent, en court circuit :

\(I_0 = \frac{E}{r}\)

D'où : \(r = r_1 + r_2 + r_3\)

Si l'un des générateurs avait été branché en sens inverse (on dit en opposition), la différence de potentiel^[3] à vide entre ses bornes aurait été égale à l'opposé de sa f.é.m.

En conclusion :

• pour la partie active du générateur équivalent, les f.é.m. s'ajoutent en valeur algébrique; elles sont comptées positivement quand elles tendent à faire remonter le potentiel dans le sens \(A \rightarrow B\), négativement quand elles tendent à faire remonter le potentiel dans le sens \(B \rightarrow A\).

• pour la partie passive du générateur équivalent, les résistances^[4] internes s'ajoutent, que les générateurs soient montés en série ou en opposition.

Des générateurs associés en série sont équivalents à un générateur unique, dont la f.é.m. a pour valeur la somme algébrique des f.é.m. des générateurs associés, et dont la resistance interne est la somme des résistances internes.

\(E_{eq}=\sum_nE_n\textrm{ (somme algébrique) }\)

\(r_{eq}=\sum_nr_n\)

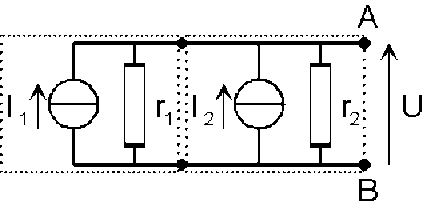
Dans ce cas, on utilise le modèle de Norton.

Si l'on relie A et B par un court circuit, la totalité du courant débité par les deux sources idéales de courant passe dans ce court circuit. Le courant maximum débité par le générateur^[1] équivalent a donc pour valeur :

\(I_0 = I_1 + I_2\)

puisque dans l'exemple étudié, les deux générateurs débitent dans le même sens; sinon, il aurait fallu choisir un sens positif et faire la somme algébrique.

A vide la différence de potentiel^[3] entre A et B est, pour l'association des deux générateurs :

\(U=\frac{I_1+I_2}{g_1+g_2}\)

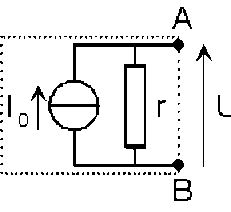
et, pour le générateur équivalent :

\(U=r.I_0=\frac{I_0}{g}\)

d'où :

\(g = g_1 + g_2\)

\(I_0=\sum_nI_n\textrm{ (somme algébrique) }\)

\(g=\sum_ng_n\)

La conductance^[5] du générateur équivalent à une association en parallèle^[6] est égale à la somme des conductances des générateurs associés; autrement dit, sa résistance^[4] interne est égale à la résistance équivalente aux deux résistances associées en parallèle. En conclusion, du point de vue actif, les courants s'ajoutent de façon algébrique; du point de vue passif^[7], les conductances s'additionnent.