Adaptation d'un générateur à sa charge
Adaptation en tension

Soit un générateur[1] de f.é.m. E et de résistance[2] interne r, chargé par une résistance R. Cherchons dans quelles conditions la tension[3] U aux bornes du générateur dépend le moins possible de R.
On choisit le modèle de Thévenin pour représenter le générateur. Le montage peut être considéré comme un générateur de tension[4] idéal de f.é.m. E alimentant un diviseur de tension[4] formé de deux dipôles[5] en série de résistances r et R. D'où :
\(U=E\frac{R}{r+R}=\frac{E}{1+\frac{r}{R}}\)
Si les deux résistances r et R vérifient la condition : \(r\ll R\), la tension aux bornes du générateur est pratiquement égale à sa f.é.m. E. On dit alors qu'il y a adaptation en tension du générateur à sa charge.
Adaptation en courant
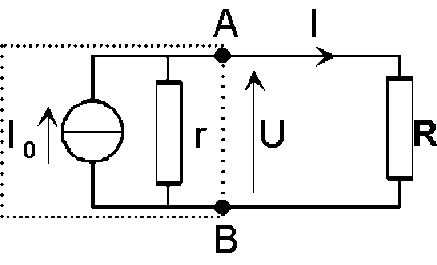
Soit un générateur[1] de f.é.m. E et de résistance[2] interne r, chargé par une résistance R. Cherchons dans quelles conditions le courant débité par le générateur dépend le moins possible de R.
On choisit le modèle de Norton pour représenter le générateur. Le montage peut être considéré comme un générateur de courant idéal débitant un courant d' intensité[6] constante \(I_0\) dans un diviseur de courant[7] formé de deux dipôles[5] en parallèle[8] de résistances r et R. D'où :
\(I=\frac{G}{g+G}I_0=\frac{I}{1+\frac{g}{G}}I_0=\frac{gE}{1+\frac{g}{G}}\)
Pour que l'intensité du courant débité par le générateur soit la plus indépendante possible de la résistance de charge, on doit avoir \(G\gg g\) ou \(R\ll r\). L'intensité est alors pratiquement égale à sa valeur maximale \(I_0 = g.E = \frac{E}{r}\). On dit alors qu'on a réalisé une adaptation en courant entre le générateur et sa charge.