Choix du schéma à utiliser
Dans l'étude des circuits comportant des éléments en série, la représentation du générateur[1] par un modèle de Thévenin, associée à l'utilisation du diviseur de tension[2], permet souvent de simplifier la résolution des problèmes.
Dans l'étude des circuits comportant des éléments en parallèle[3], c'est la représentation du générateur par un modèle de Norton, associée à l'utilisation du diviseur de courant[4], qui permet souvent de simplifier la résolution des problèmes.
Exemple :
Un générateur a une f.é.m. E = 20 V et une résistance[5] interne r = 50 \(\Omega\)
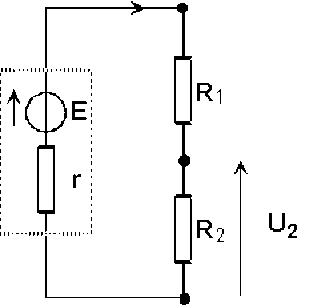
Si on utilise le modèle de Thévenin, on peut considérer qu'on a une source de tension idéale de f.é.m. E alimentant un diviseur de tension formé des 3 résistances r, \(R_1\) et \(R_2\). d'où :
\(U_2=E.\frac{R_2}{r+R_1+R_2}\)
Application numérique : \(U_2 = 5 \textrm{ V}\). On aurait trouvé la même valeur avec le modèle de Norton, mais le calcul aurait été plus long.
Le générateur alimente deux dipôles montés en parallèle, de résistances \(R_1 = 10 \;\Omega\) et \(R_2 = 20\;\Omega\). Quelle est l'intensité du courant dans \(R_2\) ?
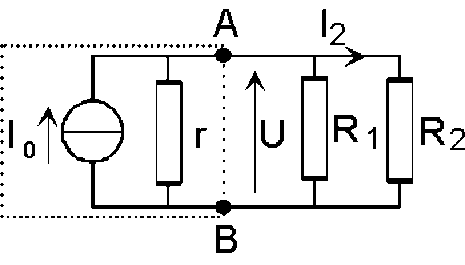
On utilise cette fois le modèle de Norton, et on peut considérer que l'on a une source de courant idéale débitant une intensité[7] \(I_0\) dans 3 dipôles en parallèle : c'est un diviseur de courant à 3 branches. D'où :
\(I_2=I_0\frac{G_2}{g+G_1+G_2}=g.E\frac{G_2}{g+G_1+G_2}\)
Application numérique : \(I_2 = 0,12 \textrm{ A}\). Avec le modèle de Thévenin, on aurait trouvé la même chose, mais après un calcul bien plus laborieux !