Schéma théorique équivalent à un générateur - Générateur de tension (3 pages)
Position du problème
Le but de ce paragraphe est de trouver une représentation symbolique d'un générateur[1] qui soit simple et qui mette bien en évidence les propriétés décrites dans les paragraphes précédents. Deux schémas sont possibles selon que l'on s'intéresse à la possibilité pour le générateur de fournir une tension[2] ou à celle de débiter un courant.
Générateur de tension (Modèle de Thevenin)
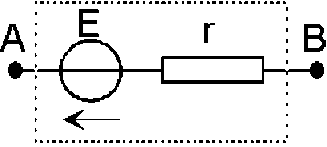
La différence (\(E - U\)) entre la f.é.m. du générateur[1] et la tension[2] effectivement disponible entre ses bornes représente les pertes internes au générateur et peut en général s'écrire: \(E - U = r.I\). D'où le schéma ci-dessus dans lequel :
le cercle représente une source de tension idéale, de résistance[3] interne nulle, qui symbolise la partie active du générateur; le sens de la flèche est dirigé vers le pôle[4] positif.
r est la résistance interne, qui représente les pertes et symbolise le côté passif du générateur.
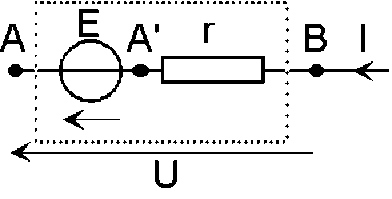
Si on le considère comme formé de deux dipôles[5] en série, on peut écrire :
\((V_A - V_B) = (V_A - V_A') + (V_A' - V_B)\)
\((V_A - V_A') = E > 0\)
puisque le potentiel du pôle positif A est plus élevé que celui du pôle négatif A'.
\((V_A' - V_B) = -r.I < 0\)
puisque le courant est dirigé de B vers A', ce qui implique le potentiel de B est supérieur à celui de A'. D'où:
\((V_A - V_B) = E - r.I\)
Le schéma restitue bien les propriétés du générateur.
Générateur de courant (Modèle de Norton)
On peut imaginer un deuxième schéma en s'intéressant au courant débité par le générateur[1] :
\(U = E - r.I \Leftrightarrow I=\frac{E}{r}-\frac{U}{r}=I_0-g.U\)
où : \(I_0 = \frac{E}{r}\) est le courant que débiterait le générateur dans un court circuit, qui est la valeur théorique maximale de l' intensité[6] que peut débiter le générateur.
et : \(g = \frac{1}{r}\) est la conductance interne du générateur.
La différence (\(I_0 - I\)) entre l'intensité maximum que peut débiter le générateur et celle qu'il débite effectivement est égale à g.U et représente les pertes en courant dans le générateur. D'où le schéma théorique suivant :
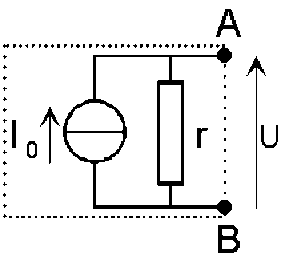
le cercle barré représente une source de courant idéale, de résistance[3] interne nulle, débitant en permanence un courant d'intensité \(I_0\) quand elle fonctionne ; c'est la partie active du générateur.
r est la résistance interne, qui représente les pertes, et symbolise la partie passive du générateur.
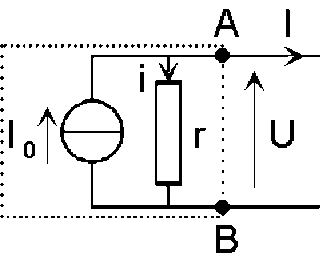
D'après ce schéma :
\(I_0 = i + I\)
\(I = I_0 - i\)
comme : \(U = r.i\) alors \(i = g.U\) ;
donc : \(I = I_0 - g.U\)
Le schéma traduit bien les propriétés du générateur.