Champ créé par un disque chargé uniformément
Durée : 5 mn
Note maximale : 10
Question
Un disque de rayon \(R\) porte une densité superficielle de charge \(\sigma\) constante.
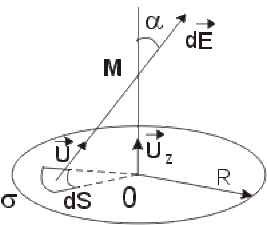
Ecrire l'intégrale permettant de calculer le champ crée par le disque en un point \(M\) de son axe.
Solution
Le champ total \(E\) est la somme des projections des champs élémentaires \(d\vec E\) sur l'axe \(Oz\) :
\(E=\displaystyle{\iint_\textrm{disque}\frac{\sigma dS}{4\pi\epsilon_0r^2}\cos\alpha}\)
Tous les éléments de surface \(dS_1, dS_2 ...\) appartenant à un même anneau apporte la même contribution au champ total (\(s , \alpha, r\) identiques)
\(E=\displaystyle{\iint_\textrm{disque} \frac{\sigma}{4\pi\epsilon_0r^2}\cos\alpha(dS_1+dS_2+...)=\int_0^R\frac{\sigma\cos\alpha}{4\pi\epsilon_0r^2}\cdot2\pi.\rho d\rho}\)
où \(2\pi\rho d\rho\) est la surface d'un anneau de rayon \(\rho\) et de largeur \(d\rho\) .