Champ créé par un disque chargé uniformément
Durée : 5 mn
Note maximale : 10
Question
Quel est le champ total créé par le disque en un point \(M\) de son axe ?
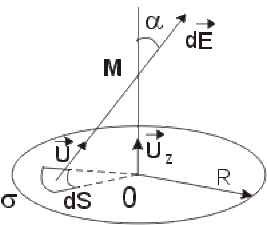
Solution
\(E=\displaystyle{\int_0^R\frac{\sigma\cos\alpha}{4\pi\epsilon_0r^2}2\pi\rho d\rho}\)
\(r=\frac z{\cos\alpha}\)
\(\rho=ztg\alpha\)
\(d\rho=z\frac{d\alpha}{\cos^2\alpha}\)
\(\alpha_{\textrm{max}}\) étant l'angle sous lequel on voit de \(M\) la périphérie du disque.
\(E=\frac{\sigma}{2\epsilon_0} \int_0^{\alpha_{\textrm{max}}}\sin\alpha d\alpha=\frac{\sigma}{2\epsilon_0}[-\cos\alpha]_0^{\alpha_{\textrm{max}}}\)
\(E=\frac{\sigma}{2\epsilon_0}(1-\cos\alpha_{\textrm{max}})\)
\(E=\frac{\sigma}{2\epsilon_0}\left(1-\frac z{\sqrt{R^2+z^2}}\right)\)