Théorème de Coulomb
Une formule simple (théorème de Coulomb) donne le champ électrique aux points très voisins de la surface d'un conducteur.
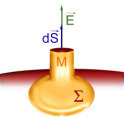
Soit un tube de champ électrique élémentaire partant de la surface du conducteur étudié. Il est perpendiculaire à la surface de ce conducteur et il délimite sur celui-ci un élément de surface d'aire \(\mathrm d S\) très petite.
Constituons une surface fermée en limitant ce tube par une section droite très voisine du conducteur et passant par le point \(M\) où l'on se propose de calculer le champ électrique. Cette section a aussi l'aire \(\mathrm d S\). A l'autre bout le tube de champ sera limité par une surface quelconque \(\Sigma\) tracée dans le conducteur.
Appliquons le théorème de Gauss à cette surface fermée. Nous avons déjà remarqué que le flux à travers un tube de champ est nul. Le flux à travers la surface \(\Sigma\) est nul aussi puisque le champ électrique est nul à l'intérieur d'un conducteur. Il reste le flux
\(\mathrm d \Phi = + E~\mathrm d S\)
La quantité d'électricité qui se trouve dans le volume considéré est répartie sur l'élément de surface que le tube de champ délimite sur le conducteur. Elle vaut donc :
\(\mathrm d q = \sigma~\mathrm d S\)
en désignant par \(\sigma\) la densité superficielle de charge sur cet élément de surface.
D'après le théorème de Gauss :
\(\mathrm d \Phi = \frac{\mathrm d q}{\epsilon_0}\)
\(E~\mathrm d S = \frac{\sigma~\mathrm d S}{\epsilon_0}\)
\(E = \frac{\sigma}{\epsilon_0}\)
En désignant par \(\vec u_n\) le vecteur unitaire normal à la surface :
\(\vec E = \frac{\sigma}{\epsilon_0}~\vec u_n\) ,
qui exprime le théorème de Coulomb.