Condensateur cylindrique 1/3
Partie
Question
Soit un condensateur cylindrique constitué de deux armatures métalliques coaxiales, d'épaisseur négligeable, de rayons respectifs \(R_A\), \(R_B\) faibles devant la hauteur \(h\).
a) Quel est le champ \(\vec E\) en un point \(M\) situé entre les armatures ?
b) Déterminer la différence \(V\) de potentiel entre les armatures.
c) Calculer la capacité du condensateur.
Aide simple
Lorsque le système d'armatures possède une symétrie élevée, il est aisé de calculer la capacité du condensateur suivant la méthodologie suivante :
On suppose une charge \(Q_A\) sur l'armature \(A\) ;
On calcule le champ \(\vec E\) entre les armatures en s'aidant du théorème de Gauss ;
On calcule la différence de potentiel : \(\displaystyle{V(A) - V(B) = - \int_B^A \vec E . \mathrm d \vec M}\)
La capacité du condensateur est donnée par le rapport : \(C = \frac{Q}{V(A) - V(B)}\)
Aide détaillée
\(\displaystyle{V(A) - V(B) = - \int_B^A \vec E . \mathrm d \vec M}\)
Il faut trouver le champ électrique \(\vec E\) à l'aide du théorème de Gauss et intégrer pour une suite de déplacement \(\mathrm d \vec M\) sur le même rayon de manière à bénéficier de l'égalité : \(\vec E . \mathrm d \vec M = \pm E ~ \mathrm d M\) selon le signe de \(\sigma_A = \frac{Q_A}{S}\) .
Rappel de cours
Voir la page Méthodologie pour le calcul de C
Solution simple
\(V(A) - V(B) = \frac{Q}{2 \pi \epsilon_0 h} \ln \left( \begin{array}{lc} \frac{R_B}{R_A} \end{array} \right) = \frac{Q_A}{C} ~~\) \(\Rightarrow ~~ C = \frac{2 \pi \epsilon_0 h}{\ln \left( \begin{array}{lc} \frac{R_B}{R_A} \end{array} \right)}\)
Solution détaillée
a)
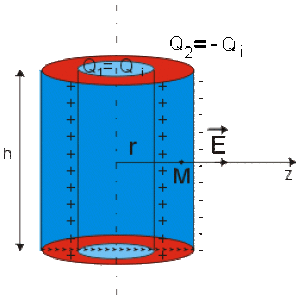
Le flux du champ électrique à travers une surface cylindrique de rayon \(r\) fermée aux deux extrémités par deux disques de surface \(S_{e_1}\) et \(S_{e_2}\), et de surface latérale \(S_L\) est :
\(\Phi = \frac{Q_i}{\epsilon_0} = \iint_{S_{e_1}} \vec E . \mathrm d \vec S + \iint_{S_{e_2}} \vec E . \mathrm d \vec S + \iint_{S_L} \vec E . \mathrm d \vec S\)
En tout point des surfaces perpendiculaires à l'axe, par symétrie : \(\mathrm d \vec S \perp\vec E\) . Les deux premières intégrales sont donc nulles alors qu'en tout point de la surface latérale \(S_L\), \(\vec E\) est constant et colinéaire à \(\mathrm d \vec S\) d'où :
\(\Phi = \frac{Q_i}{\epsilon_0} = E \iint \mathrm d S\)
\(\frac{Q_i}{\epsilon_0} = E ~ (2 \pi r h)~~\) soit \(E = \frac{Q_i}{2 \pi \epsilon_0 r h}\)
La charge intérieure \(Q_i\) est la charge \(Q_A\) de l'armature \(A\).
b)
\(\displaystyle{V(A) - V(B) = - \int_B^A \vec E . \mathrm d \vec M = - \frac{Q_A}{2 \pi \epsilon_0 h} \int_{R_B}^{R_A} \frac{\mathrm d r}{r} = - \frac{Q_A}{2 \pi \epsilon_0 h} [\ln r]_{R_B}^{R_A} }\)
c)
\(V(A) - V(B) = \frac{Q}{2 \pi \epsilon_0 h} \ln \left( \begin{array}{lc} \frac{R_B}{R_A} \end{array} \right) = \frac{Q_A}{C} ~~\) \(\Rightarrow ~~ C = \frac{2 \pi \epsilon_0 h}{\ln \left( \begin{array}{lc} \frac{R_B}{R_A} \end{array} \right)}\)