Equivalence : condensateur cylindrique - condensateur plan 3/3
Partie
Question
Le coefficient de capacité d'un condensateur cylindrique constitué de deux armatures coaxiales de rayons \(R_A\) et \(R_B\) est
\(C = \frac{2 \pi \epsilon_0 h}{\ln \left( \begin{array}{lc} \frac{R_B}{R_A} \end{array} \right)}\)
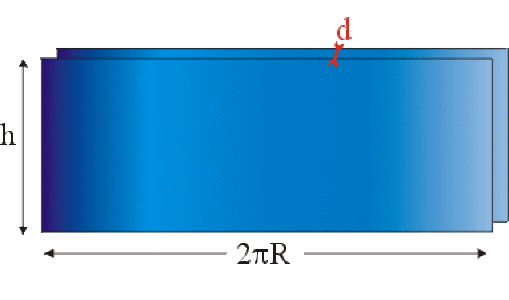
Vérifier que pour une faible distance \(R_B - R_A\) entre les armatures, le coefficient de capacité \(C\) obtenu est identique à celui d'un condensateur plan de même surface que le condensateur obtenu en deroulant à plat les armatures du condensateur cylindrique.
Rappel de cours
Voir la page Méthodologie pour le calcul de C
Solution détaillée
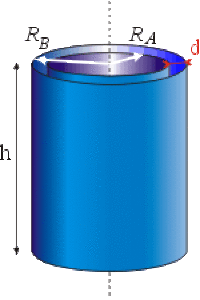
équivalence électrique
Posons \(R_B - R_A = d\)
où \(R_B = R_A \Big( 1 + \frac{d}{R_A} \Big)\)
\(\frac{d}{R_A} \ll 1 ~ \); \(~ \ln \frac{R_B}{R_A} = \ln \Big( 1 + \frac{d}{R_A} \Big) \approx 1 + \frac{d}{R_A}\)
\(C \approx \frac{2 \pi \epsilon_0 h R_A}{d} = \frac{\epsilon_0 \big(2 \pi R_A h\big) }{d} = \frac{\epsilon_0 S}{d}\)
où \(S\) est la surface de l'armature.