Condensateur sphérique 2/3
Partie
Question
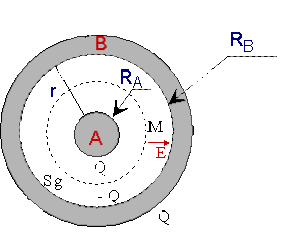
Deux conducteurs sphériques concentriques \(A\) et \(B\) forment un condensateur.
Soit \(R_A\) le rayon extérieur de \(A\) et \(R_B\) le rayon intérieur de \(B\) .
a) Quel est le champ \(\vec E\) en un point \(M\) situé entre les armatures ?
b) Déterminer la différence de potentiel \(V(A) - V(B)\) entre les armatures.
c) Calculer le coefficient de capacité du condensateur.
Rappel de cours
Voir la page Méthodologie pour le calcul de C
Solution simple
a) \(E = \frac{Q}{4 \pi \epsilon_0 r^2}\)
b) \(V(A) - V(B) = \frac{Q_A}{4 \pi \epsilon_0} \left( \begin{array}{lc} \frac{R_B - R_A}{R_B ~ R_A} \end{array} \right)\)
c) \(C = 4 \pi \epsilon_0 \left( \begin{array}{lc} \frac{R_B ~ R_A}{R_B - R_A} \end{array} \right)\)
Solution détaillée
a)
Par symétrie, le champ \(\vec E\) est radial. Traçons une sphère de Gauss \(Sg\) de rayon \(R\) passant par \(M\) .
Le flux de \(\vec E\) à travers \(Sg\) est : \(\Phi = \iint_{Sg} \vec E . \mathrm d \vec S = E ~ 4 \pi r^2\)
Si la sphère \(A\) porte la charge \(Q_A\) le Théorème de Gauss donne :
\(E ~ 4 \pi r^2 = \frac{Q}{\epsilon_0} ~~\) \(\Rightarrow ~~ E = \frac{Q}{4 \pi \epsilon_0 r^2}\)
b)
\(\displaystyle{V(A) - V(B) = - \int_{R_B}^{R_A} \vec E . \mathrm d \vec M = - \int_{R_B}^{R_A} \vec E . \mathrm d r}\)
Pour un déplacement radial de \(M\), \(\vec E \parallel \mathrm d \vec r\) donc :
\(\displaystyle{V(A) - V(B) = - \int_{R_B}^{R_A} E ~ \mathrm d R}\)
\(V(A) - V(B) = \frac{Q_A}{4 \pi \epsilon_0} \left( \begin{array}{lc} \frac{R_B - R_A}{R_B ~ R_A} \end{array} \right)\)
c)
\(V(A) - V(B) = \frac{Q_A}{C} = \frac{Q_A}{4 \pi \epsilon_0} \left( \begin{array}{lc} \frac{R_B - R_A}{R_B ~ R_A} \end{array} \right)\)
\(C = 4 \pi \epsilon_0 \left( \begin{array}{lc} \frac{R_B ~ R_A}{R_B - R_A} \end{array} \right)\)
On note que l'on retrouve le coefficient de capacité d'un condensateur plan \(C = \frac{\epsilon_0 S}{e}\) si \((R_B - R_A) < R_A, R_B\)
\(R_1 R_2 \approx R^2\) avec \(e = R_B - R_A\) car \(S = 4 \pi R^2\) est la surface de la sphère.