Effet dipolaire / Caractériser un dipôle électrique
Description d'un dipôle électrique
Dans un grand nombre de molécules on observe que la charge totale du système électrique se conserve (principe de conservation de la charge d'un système). Ceci n'exclut pas, malgré l'existence simultanée d'un ion et de son contre ion (système électriquement neutre), que nous ayons des délocalisations microscopiques de charges positives et négatives.
On appelle dipôle électrique un système de 2 charges de même quantité d'électricité \(q\), de signes opposés distantes de \(a\).
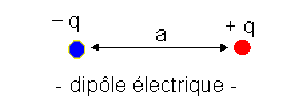
Le moment dipolaire d'un dipôle électrique
En désignant par \(A\) le centre des charges négatives \(- q\) et par \(B\) le centre des charges positives \(+ q\), on définit géométriquement dans ce sens, le vecteur :
\(\vec a = \overrightarrow{AB}\) .
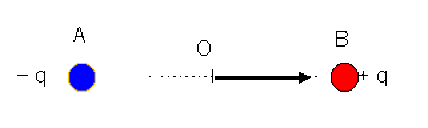
Toujours selon le sens géométrique choisi (de la charge négative vers la charge positive) on caractérise le moment dipolaire du dipôle électrique par la grandeur vectorielle :
\(\vec p = q ~ \times ~ \vec a\)
Le vecteur \(\vec p\) a pour origine \(O\) le centre du dipôle.
Le moment dipolaire du physicien et le moment dipolaire du chimiste.
La convention adoptée ici par les physiciens a été choisie en conformité avec les règles d'orientation des espaces vectoriels en mathématiques.
En chimie, dans le but de rappeler que l'électron est l'élément responsable de l'association entre deux atomes, il a été choisi un sens du dipôle qui va dans le sens du déplacement des charges négatives lors d'une réaction. L'étudiant se souviendra de ces choix d'orientation tout à fait justifiables et se gardera de toute confusion.
Unité de moment dipolaire :
L'unité de moment dipolaire dans le système S.I. s'obtient par l'analyse des dimensions des grandeurs qui le définissent. \(\vec p\) a pour unité le coulomb.mètre. Symbole \(C.m\)
Unité pratique de moment dipolaire.
A l'échelle moléculaire les charges électriques sont de l'ordre de grandeur de la charge de l'électron ou du proton tandis que les distances sont de l'ordre de l'Angström. Le debye, symbole D, défini par :
\(p = q.a\)
est alors voisin de \(1,6.10^{-19} ~ \times ~ 1.10^{-10} = 1,6.10^{-29} ~ \mathrm{C.m}\) .
A l'échelle moléculaire on adoptera le debye :
\(1 ~ \mathrm D = \frac{1}{3}.10^{-29} ~ \mathrm{C.m}\)
Cette unité est bien adaptée au domaine de la Chimie et à l'étude des molécules.
En effet si \(a=1\stackrel{\circ}{\mathrm A}\) et \(q = 1,6.10^{-19} ~ \mathrm C\), alors nous avons \(p = 1,6.10^{-29} ~ \mathrm{C.m}\), soit \(p = 4,8 ~ \mathrm D\).
Exemple :
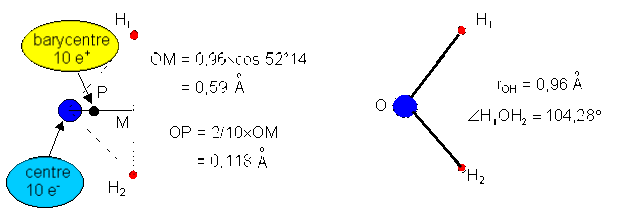
Exemple de dipôle : La molécule ''polaire'' \(\mathrm H_2 \mathrm O\).
L'association de 2 atomes d'hydrogène et d'un atome d'oxygène conduit dans certaines conditions expérimentales à la formation d'une molécule d'eau.
Le système de charges, protons plus électrons obtenu présente un moment dipolaire permanent. Au cours de la formation de la molécule d'eau, l'atome d'hydrogène est donneur tandis que l'atome d'oxygène est accepteur.
Le centre \(N\) des 10 charges négatives et le centre \(P\) des 10 charges positives sont distincts.
On mesure pour la molécule polaire \(\mathrm H_2 \mathrm O\) un moment \(p = 6,2.10^{-30} ~ \mathrm{C.m}\), soit \(1,86 ~ \mathrm D\).
Si \(~|\vec p| = 10~e ~\times~a\) ,
Il s'en suit que \(a = 0,039.10^{-12} ~ \textrm{m\`etre}\), ou \(a = 3,9.10^{-2} ~ \stackrel{\circ}{\mathrm A}\) .
Exercice résolu :
La molécule d'eau \(\mathrm H_2 \mathrm O\) possède un ensemble de charges de 10 électrons et 10 protons. Afin de mieux comprendre l'existence du moment dipolaire permanent de la molécule d'eau nous étudierons un modèle qui accentue le caractère donneur des atomes d'hydrogène en supposant que leurs électrons sont venus combler entièrement les sites vacants de l'atome d'oxygène. Calculer le moment dipolaire que l'on obtiendrait dans cette hypothèse.
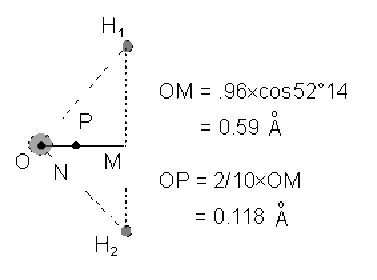
Dans l'hypothèse de ce modèle les barycentres des 10 électrons et des 10 protons sont distants de \(0,118\stackrel{\circ}{\mathrm A}\), ce qui conférerait à notre molécule un moment dipolaire :
\(p = q.a\)
ou \(~p = 10~\times~1,6.10^{-19}~\times~0,118.10^{-10} = 1,89.10^{-29} ~ \mathrm{C.m}\)
soit : \(~p = 5,67 ~ \mathrm D\)
La valeur exagérée de ce résultat par rapport à la réalité provient du fait que les électrons des atomes d'hydrogène ne sont que partiellement délocalisés sur l'atome d'oxygène.