Interférences localisées. Lames minces

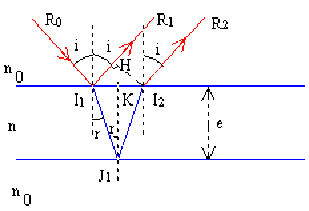
Calculons la différence de marche géométrique entre deux rayons réfléchis successifs.

Une surface d'onde est définie comme étant le lieu des points \(M\) pour lesquels les trajets optiques des rayons lumineux calculés à partir d'un point source ou d'un point image sont identiques.

Entre deux surfaces d'onde d'un faisceau lumineux les trajets optiques des rayons constituant le faisceau sont identiques.

Pour un faisceau de rayons parallèles, les surfaces d'onde sont les plans perpendiculaires au faisceau.

Considérons les rayons \(R_1\) et \(R_2\). Le plan passant par les points \(I_2\) et \(H\) est un plan d'onde puisque les rayons \(R_1\) et \(R_2\) sont parallèles. Les trajets optiques des rayons \(R_1\) et \(R_2\) sont donc identiques à partir de ce plan d'onde jusqu'au point image situé à l'infini.

Les rayons \(R_1\) et \(R_2\)sont issus d'un même rayon \(R_0\). La différence de marche entre ces deux rayons provient des trajets optiques \((I_1H)\) de \(R_1\) dans l'air et \((I_1J_1I_2)\) de \(R_2\) dans le verre. Les rayons \(R_1\) et \(R_2\) sont issus d'un même rayon \(R_0\). La différence de marche entre ces deux rayons provient des trajets optiques \((I_1H)\) de \(R_1\) dans l'air et \((I_1J_1I_2)\) de \(R_2\) dans le verre.

d'où \(\delta = (I_1J_1I_2) - (I_1H)\)

or \((I_1J_1I_2) = 2 (I_1J_1) = \frac{2 n e}{\cos r}\)

Avec \( n_0 \sin i = n \sin r\)

\((I_1H ) = n_0 I_1 \sin i = 2 I_1K \sin i . n_0\) et \(I_1K =  e \tan r\) d'où :

\(\begin{array}{r c l} \delta&=&\displaystyle{ \frac{2ne}{e\cos r}-2e.\tan r.\sin i.n=2ne\left(\frac{1}{\cos r}-\tan r.\sin r\right)} \\\\ &=&2ne\cos r\end{array}\)

La différence de marche ondulatoire doit de plus tenir compte des changements de signe éventuels à la réflexion. En effet la réflexion d'un rayon lumineux provenant d'un milieu moins réfringent sur un milieu plus réfringent introduit un déphasage de \(\pi\), soit une différence de marche supplémentaire de \(\lambda / 2\) (ce résultat, que nous admettrons, se démontre à partir des équations de Maxwell ).

La différence de marche ondulatoire s'écrit pour deux rayons transmis consécutifs:  \(dr = 2 n e \cos r\) et pour deux rayons réfléchis consécutifs: \(dr = 2 n e \cos r + \lambda/2\)