Interférences localisées. Lames minces

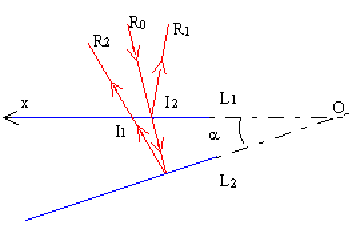
Si l'épaisseur e est faible et si l'angle a du coin d'air est petit , le rayon réfléchi \(R_2\) émerge en \(I_2\) très près du point d'incidence \(I_1\) et l'on considère alors que l'épaisseur reste quasiment constante entre \(I_1\) et \(I_2\). On peut alors écrire la différence de marche à partir du calcul fait pour les lames à faces parallèles:

\(\delta = 2 n e \cos r + \frac{\lambda}{2}\)

L'angle \(i\) est faible or \(n \sin r = \sin i \), l'angle \(r\) est faible et \(\cos r = 1\). D'où :

\(\delta = 2 n e \cos r + \frac{\lambda}{2} \approx 2 n e +\frac{\lambda}{2} = 2 n \alpha x + \frac{\lambda}{2}\)

on peut calculer l'interfrange \(\Delta x: \quad2 n\, \alpha \,\Delta x = \lambda\) soit \(\Delta x= \frac{\lambda}{2 n \alpha}\)