Le champ magnétostatique

représentant les effets physiques d'une distribution, par rapport à un plan de symétrie et par rapport à un plan d'antisymétrie de cette distribution

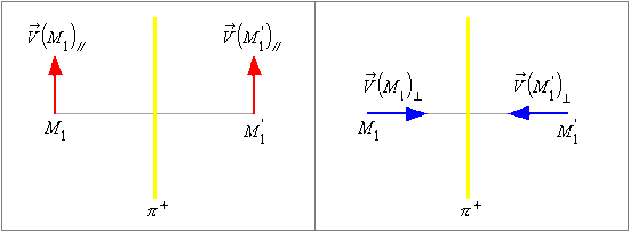
• Effets de la distribution \(\mathfrak{(D)}\) en deux points \(M_1\) et \(M^,_1\) symétriques par rapport à l'un des plans de symétrie ou par rapport à l'un des plans d'antisymétrie de \(\mathfrak{(D)}\).

  Les effets physiques de \(\mathfrak{(D)}\) en un point \(\mathsf{M}\) étant représentés par le vecteur \(\vec V(M)\), soit \(\vec V(M_1)\) l'effet de \(\mathfrak{(D)}\) en \(M_1\) et \(\vec V(M^,_1)\) l'effet de \(\mathfrak{(D)}\) en\( M^,_1\)

• Dans le cas où la distribution \(\mathfrak{(D)}\) possède un plan de symétrie positive \((\pi^+)\) :

  \(\vec V(M_1)_{//} = \vec V(M^,_1)_{//}\) et \(\vec V(M_1)_{ \perp} = -\vec V(M^,_1)_ \perp\)

• Dans le cas où la distribution \(\mathfrak{(D)}\) possède un plan de symétrie négative \((\pi^-)\) :

  \(\vec V(M_1)_{//} = -\vec V(M^,_1)_{//}\) et \(\vec V(M_1)_{ \perp} = \vec V(M^,_1)_ \perp\)

• Effets de la distribution \(\mathfrak{(D)}\) en un point \(\mathsf{M}\) appartenant à l'un des plans de symétrie ou à l'un des plans d'antisymétrie de \(\mathfrak{(D)}\).

  • Dans le cas où la distribution \(\mathfrak{(D)}\) possède un plan de symétrie positive \((\pi^+)\) :

    le vecteur représentant les effets de cette distribution doit rester inchangé : \(\vec V(M)_{\perp} = \vec 0\)

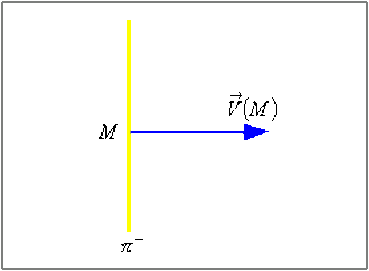
• Dans le cas où la distribution \(\mathfrak{(D)}\) possède un plan de symétrie négative \((\pi^-)\) :

  le vecteur représentant les effets de cette distribution doit changer de signe : \(\vec V(M)_{//} = \vec 0\)

quand les effets d'une distribution sont représentés par un vecteur vrai, ce vecteur est contenu dans les plans de symétrie positive de la distribution et est perpendiculaire aux plans de symétrie négative.