Le champ magnétostatique

représentant les effets physiques d'une distribution, par rapport à un plan de symétrie et par rapport à un plan d'antisymétrie de cette distribution

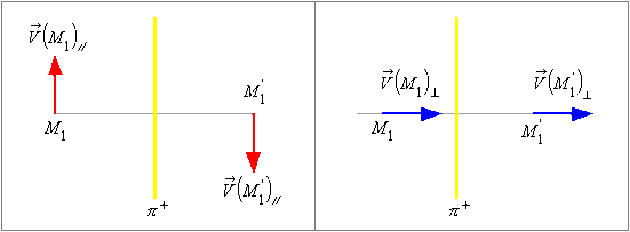
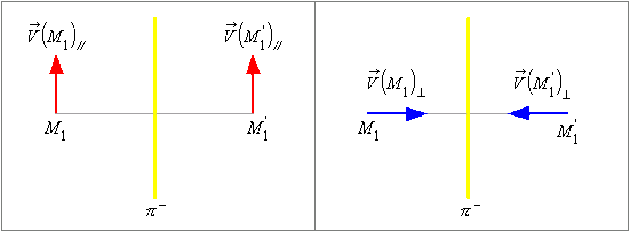
• Effets de la distribution \(\mathfrak{(D)}\) en deux points \(M_1\) et \(M^,_1\) symétriques par rapport à l'un des plans de symétrie ou par rapport à l'un des plans d'antisymétrie de \(\mathfrak{(D)}\).

  Les effets physiques de \(\mathfrak{(D)}\) en un point \(\mathsf{M}\) étant représentés par le pseudo-vecteur \(\stackrel{\hookrightarrow}{V}(M)\), soit \(\stackrel{\hookrightarrow}{V}(M_1)\) l'effet de \(\mathfrak{D}\) en \(M_1\) et \(\stackrel{\hookrightarrow}{V}(M'_1)\) l'effet de \(\mathfrak{(D)}\) en \(M^,_1\).

• Dans le cas où la distribution \(\mathfrak{(D)}\) possède un plan de symétrie positive (\(\pi^+\)) :

  \(\vec V(M_1)_{//} =- \vec V(M^,_1)_{//}\) et \(\vec V(M_1)_{\perp} = \vec V(M^,_1)_{\perp}\)

• Dans le cas où la distribution \(\mathfrak{(D)}\) possède un plan de symétrie négative \((\pi^-)\) :

  \(\vec V(M_1)_{//} = \vec V(M^,_1)_{//}\) et \(\vec V(M_1)_{\perp} =- \vec V(M^,_1)_{\perp}\)

• Effets de la distribution \(\mathfrak{(D)}\) en un point \(\mathsf{M}\) appartenant à l'un des plans de symétrie ou à l'un des plans d'antisymétrie de \(\mathfrak{(D)}\).

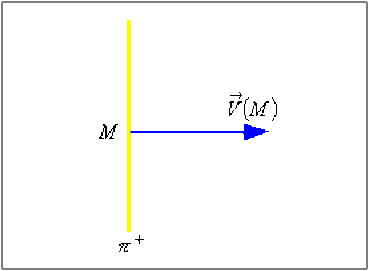
  • Dans le cas où la distribution \(\mathfrak{(D)}\) possède un plan de symétrie positive \((\pi^+)\) :

    le vecteur représentant les effets de cette distribution doit rester inchangé : \(\vec V(M)_{//} = \vec 0\)

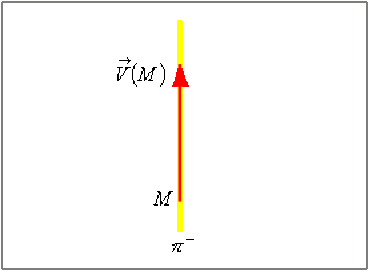
• Dans le cas où la distribution \(\mathfrak{(D)}\) possède un plan de symétrie négative \((\pi^-)\) :

  le vecteur représentant les effets de cette distribution doit changer de signe : \(\vec V(M)_{\perp} = \vec 0\)

quand les effets d'une distribution sont représentés par un pseudo-vecteur, ce dernier est contenu dans les plans de symétrie négative de la distribution et perpendiculaire aux plans de symétrie positive.