Champ de gravitation

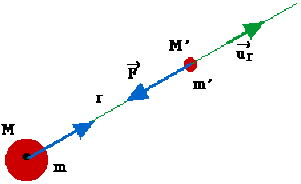
Si l'on considère deux masses ponctuelles \(m\) et \(m'\) aux points \(M\) et \(M'\), le vecteur \(\displaystyle{\overrightarrow{MM}}\) est noté \(\displaystyle{\overrightarrow r}\) et on choisit un vecteur unitaire sur \(\displaystyle{\overrightarrow{MM}}\) tel que:

\(\displaystyle{\overrightarrow{u_r}=\frac{\overrightarrow r}{r}}\)

La loi de Newton postule que la force d'interaction à distance exercée par la masse \(m\) sur \(m'\) est attractive, dépend de la distance entre les points et des masses des points matériels.

Elle décroît comme l'inverse du carré de la distance.

\(\displaystyle{\overrightarrow F(M')=-G\frac{mm'}{r^2}\overrightarrow u_r}\)

\(G\) s'appelle la constante de gravitation universelle ; cette constante a une dimension.

Dans le système S I, elle vaut:

\(G = 6, 670 . 10^{-11} \textrm{N.m}^2 \textrm{kg}\)

Cette loi de l'attraction universelle obéit au principe de l'action et de la réaction : la force exercée par \(m'\) sur \(m\) est

\(\displaystyle{\overrightarrow F'(M)=-\overrightarrow F(M')}\).

Remarque: Les masses étant positives, la force de gravitation est toujours une force d'attraction.

Il existe d'autres champs de forces en \(\displaystyle{\frac{1}{r^2}}\) ; par exemple la force d'interaction entre charges électriques dite force de Coulomb: une charge électrique \(q\) en \(M\) exerce sur une autre charge \(q'\) en \(M'\) une force :

\(\displaystyle{\overrightarrow F=\frac{1}{4\pi\epsilon_0}\frac{qq'}{r^2}\overrightarrow u_r}\).

La seule différence formelle avec la loi de Newton est que les charges électriques pouvant être positives ou négatives, la force de Coulomb est attractive ou répulsive. Mais les intensités de ces forces sont très différentes : la force coulombienne est plus intense que la force de gravitation .

Reprenons les deux masses \(m\) et \(m'\) précédentes ; \(m\) exerce sur \(m'\) une force:

\(\displaystyle{\overrightarrow F(M')=-G\frac{mm'}{r^2}\overrightarrow u_r}\)

Écrivons cette force sous la forme: \(\displaystyle{\overrightarrow F=m'\overrightarrow A(M')}\)

Nous disons que \(\displaystyle{\overrightarrow A(M')}\) est le champ de gravitation créé par \(m\) au point \(M'\); \(m\) est la source du champ (ici ponctuelle), \(m'\) est une masse test dite masse d'épreuve qui permet de détecter le champ en \(M'\) par la force qu'il exerce sur \(m'\). Une source ponctuelle de champ crée dans l'espace qui l'entoure à une distance \(r\), un champ de gravitation :

\(\displaystyle{\overrightarrow A=-G\frac{m}{r^2}\overrightarrow u_r}\)

La norme du champ de gravitation a la dimension d'une accélération, on dit aussi que c'est un champ d'accélération.

Considérons une masse \(m_1\) en \(M_1\) et une masse \(m'\) en \(M'\) telles que \(\displaystyle{\overrightarrow{M_1M'}=\overrightarrow r_1}\), la force de gravitation exercée par \(m_1\) sur \(m'\) est :

\(\displaystyle{\overrightarrow F_1=-G\frac{m_1m'}{r_1^2}\overrightarrow u_{r_1}}\)

De même la force exercée par une masse \(m_2\) en \(M_2\) sur \(m'\) est:

\(\displaystyle{\overrightarrow F_2=-G\frac{m_2m'}{r_2^2}\overrightarrow u_{r_2}}\)

Si nous envisageons les trois masses \(m_1\), \(m_2\) et \(m'\) simultanément en présence, la force exercée par \(m_1\) et \(m_2\) sur \(m'\) est la somme vectorielle des deux précédentes

\(\displaystyle{\overrightarrow F=\overrightarrow F_1+\overrightarrow F_2}\)

Cette affirmation tient compte du principe d'additivité des forces mais suppose également que la présence de \(m_2\) ne modifie pas la force exercée par \(m_1\) sur \(m'\) ; cette deuxième hypothèse constitue le principe de superposition.

Il résulte de ces deux principes que le champ créé en \(M\) par une distribution discrète de masses ponctuelles \(m\) placées en \(M\) est donné par la relation suivante:

\(\displaystyle{\overrightarrow A=-\sum_{i=1}^NG\frac{m_i}{r_i^2}\overrightarrow u_{r_i}\textrm{ avec : }\overrightarrow r_i=\overrightarrow{M_iM}\textrm{ et }\overrightarrow{u_{r_i}}=\frac{\overrightarrow r_i}{r_i} }\)

Dans le cas d'une distribution volumique continue, il faut faire la somme en \(M\) des champs élémentaires créés par chaque élément de volume \(dv\) contenant la masse \(\textrm{dm} =\rho \textrm{ dv}\) (\(\rho\) étant la masse volumique qui dépend en général de la position de \(dm\))

\(\displaystyle{\overrightarrow{dA}=-G\frac{dm}{r^2}\overrightarrow u_r\textrm{ et }\overrightarrow A(M)=-G\int_{(V)}\frac{\rho dv}{r^2}\overrightarrow u_r}\)

l'intégrale étant étendue au volume occupé par la masse répartie.

On admettra le résultat suivant:

Si la répartition des masses a la symétrie sphérique, le champ créé à l'extérieur de cette répartition est identique à celui d'une masse ponctuelle placée au centre de la sphère où serait concentrée la masse totale.