Oscillations

La solution "oscillation harmonique" est de la forme :

\(x(t) = A \cos \omega_0t + B \sin \omega_0t\)

ou sous une autre forme courante équivalente :

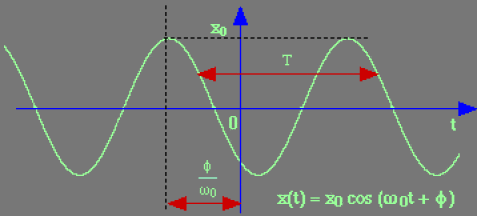
\(x(t) = x_0 \cos (\omega_0t + \emptyset)\)

avec \(\displaystyle{\omega_0=\sqrt{\frac{K}{m}}}\) est la pulsation et \(\displaystyle{T=\frac{2\pi}{\omega_0}}\)

la période de l'oscillation.

L'animation ci-dessous montre le mouvement d'une masse au bout d'un ressort en l'absence de frottement.

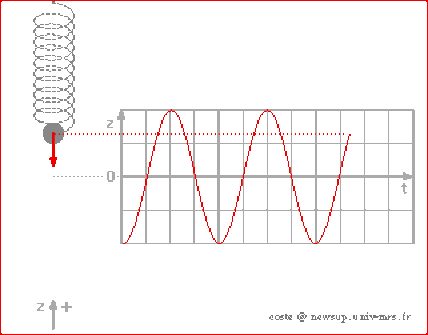
Les conditions initiales (position et vitesse) permettent de déterminer les constantes \(A\) et \(B\) ou \(x_0\) et \(\emptyset\) ( position initiale et phase initiale ).

Si on suppose que le mouvement est freiné par une force opposée à la vitesse :

\(\displaystyle{\overrightarrow f=-\alpha\dot x\overrightarrow i}\)

l'équation est :\( \displaystyle{m\ddot x=-\alpha\dot x-kx}\)

\(\displaystyle{\ddot x+\frac{\alpha}{m}\dot x+\frac{k}{m}x=0}\)

et en posant : \(\displaystyle{2\lambda=\frac{\alpha}{m}\textrm{ et }\omega_o^2=\frac{k}{m}}\)

\(\displaystyle{\ddot x+2\lambda\dot x+\omega_0^2x=0}\)

Cette équation différentielle homogène du second ordre à coefficients constants admet une solution générale de la forme :

\(\displaystyle{x(t)=A_1\textrm{e}^{r_1t}+A_2\textrm{e}^{r_2t}}\)

où \(r_1\) et \(r_2\) sont solutions de l'équation caractéristique \(\displaystyle{r^2+2\lambda r+\omega_0^2=0}\)

\(A_1\) et\( A_2\) constantes d'intégration déterminées par les conditions initiales.

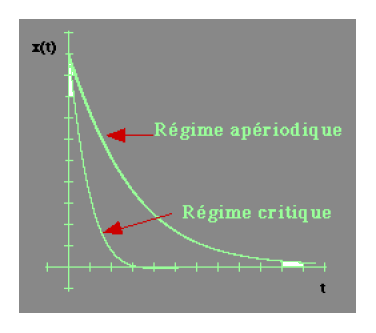
1)Quand les racines de l'équation caractéristique sont réelles, elles sont négatives et le mouvement est amorti ; le retour à l'équilibre est lent : il est apériodique

\(\displaystyle{x(t)=A_1\textrm e^{r_1t}+A_2\textrm e^{r_2t}}\)

2)La racine double négative \(r_1 = - \lambda\) correspond à "l'amortissement critique".

C'est la limite entre l'amortissement et les oscillations.

\(\displaystyle{x(t)=(A_1+A_2t)\textrm e^{-\lambda t}}\)

Ce cas correspond au retour le plus rapide à l'équilibre.

3) Si les racines imaginaires sont conjuguées, on obtient une solution oscillatoire amortie

\(\displaystyle{x(t)\textrm e^{\lambda t}\cos(\omega t+\emptyset)}\)

La constante \(\lambda\) ayant la dimension de l'inverse d'un temps , on pose \(\displaystyle{\frac{1}{\lambda}=\tau}\) la constante de temps du système ( ou temps d'amortissement).

On a alors : \(\displaystyle{x(t)=A\textrm e^{-t/\tau}\cos(\omega t+\emptyset)}\) avec \(\displaystyle{\omega=\sqrt{\omega_0^2-\lambda^2}}\)

\(\displaystyle{T=\frac{2\pi}{\sqrt{\omega_0^2-\lambda}}}\) est la pseudo période.

Le mouvement n'est pas périodique mais il en diffère peu si l'amortissement est faible.

Il est dit périodique amorti exponentiellement.

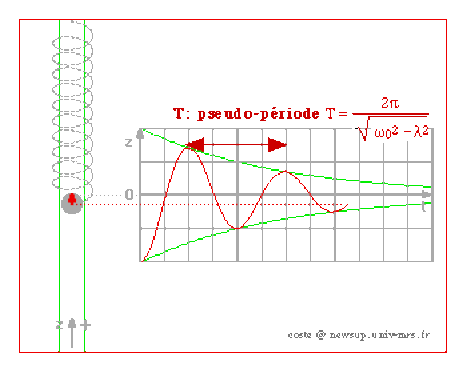
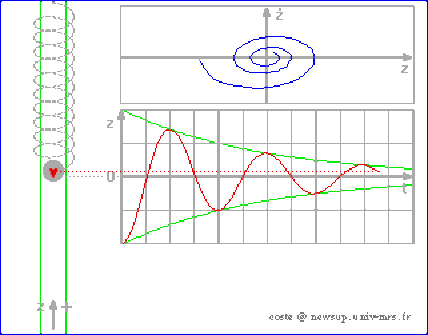
L'animation ci-dessous montre le mouvement d'une masse au bout d'un ressort en présence de frottement visqueux? L'espace de phases défini ci-dessous se trace simultanément

Il arrive qu'on représente le régime de fonctionnement d'un système dans un espace plan \(\displaystyle{(q,\frac{\textrm dq}{\textrm{dt}})}\) ou \(\displaystyle{(x,\frac{\textrm dx}{\textrm{dt}})}\)

dans lequel l'abscisse est une variable de position telle que l'élongation du ressort ou la charge du condensateur, et l'ordonnée, une variable de vitesse telle la vitesse de la masse dans le système masse-ressort ou l'intensité dans le système auto-inductance-condensateur.

Un tel espace se nomme espace des phases.

La représentation donne alors pour le régime oscillant amorti une courbe du type de celle en bleu dans la figure ci-dessous.