Construction des rayons (1)
Partie
Question
Construire géométriquement le rayon réfracté résultant du passage de la lumière d'un milieu 1 à un milieu 2 plus réfringent \((n_2>n_1)\).
Que se passe-t-il dans le cas de l'incidence rasante?
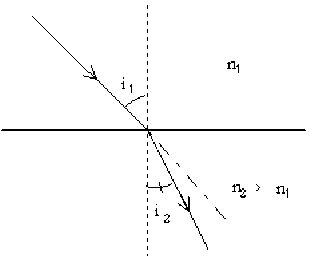
Appliquer la loi de réfraction de Descartes
Aide simple
Faire la construction géométrique du rayon réfracté en traçant deux cercles de rayons \(n_1\) et \(n_2\) centrés au point d'incidence I.
Rappel de cours
Le rayon réfracté est dans le plan d'incidence, le rayon incident et le rayon réfracté étant de part et d'autre de la normale au point d'incidence.
Pour chaque lumière monochromatique, il existe un rapport constant positif, entre les sinus des angles d'incidence et de réfraction :
\(\frac{\sin i_1}{\sin i_2}=n_{2,1}=\frac{n_2}{n_1}\)
Un rayon lumineux peut toujours passer d'un milieu transparent dans un autre plus réfringent que le premier. Dans ce cas il se rapproche de la normale (sauf si l'angle d'incidence est nul). L'angle de réfraction est au maximum égal à la valeur de l'angle limite \(\lambda\) défini par :
\(\sin\lambda=\frac{n_1}{n_2}\) avec \(\lambda < 90^{\circ}\)
Solution détaillée
Reprenons la loi de la réfraction :
\(n_1\sin i_1=n_2\sin i_2\) alors \(n_2 > n_1\Rightarrow i_2 < i_1\) le rayon réfracté se rapproche de la normale.Nous retiendrons que :
Lorsqu'un rayon passe d'un milieu moins réfringent vers un milieu plus réfringent il se rapproche de la normale.
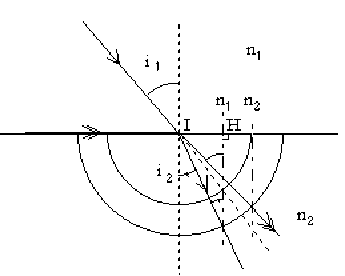
Faisons la construction géométrique du rayon réfracté.Pour ce faire nous traçons deux cercles de rayons \(n_1\) et \(n2\) centrés au point d'incidence \(I\). Nous cherchons l'intersection du prolongement du rayon incident dans le milieu d'indice \(n_1\) avec le cercle de rayon \(n_1\) et de ce point nous abaissons une perpendiculaire en \(H\) au dioptre séparant les milieux d'indice \(n_1\) et \(n_2\). Nous prolongeons cette normale jusqu'à ce qu'elle coupe le cercle de rayon \(n_2\), point par lequel passera le rayon réfracté dans le milieu d'indice \(n_2\).
Justifions la construction. Nous avons : \(\sin i_1=\frac{IH}{n_1}\) et \(\sin i_2=\frac{IH}{n_2}\). Il est simple d'en déduire que \(n_1\sin i_1=n_2\sin i_2\)
Supposons que le rayon incident attaque le dioptre en incidence rasante soit : \(i_1=\frac\pi2\) alors : \(\sin i_2=\frac{n_1}{n_2}\) et \(i_2\) est appelé angle limite, soit : \(\sin\lambda=\frac{n_1}{n_2}\)