Rayons perpendiculaires
Partie
Question
Un rayon incident arrive sur la surface libre d'un liquide d'indice \(n\).
Quel doit être l'angle d'incidence pour que le rayon réfléchi et le rayon réfracté soient perpendiculaires (A.N : n=4/3).
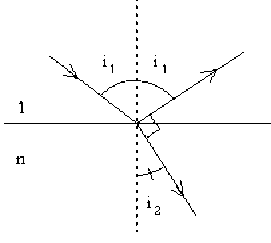
Appliquer les lois de la réfraction.
Rappel de cours
Le rayon réfracté est dans le plan d'incidence, le rayon incident et le rayon réfracté étant de part et d'autre de la normale au point d'incidence.
Pour chaque lumière monochromatique, il existe un rapport constant positif, entre les sinus des angles d'incidence et de réfraction :
\(\frac{\sin i_1}{\sin i_2}=n_{2,1}=\frac{n_2}{n_1}\)
Un rayon lumineux peut toujours passer d'un milieu transparent dans un autre plus réfringent que le premier. Dans ce cas il se rapproche de la normale (sauf si l'angle d'incidence est nul). L'angle de réfraction est au maximum égal à la valeur de l'angle limite \(\lambda\) défini par :
\(\sin\lambda=\frac{n_1}{n_2}\) avec \(\lambda< 90°\)
Solution détaillée
nous pouvons écrire que : \(i_1+i_2=\frac\pi2\)
\(1.\sin i_1=n.\sin i_2\)
\(\sin i_1=n.\sin(\frac\pi2-i_1)=n.\cos i_1\)
\(\tan i_1=n=\frac43\)
on en déduit : \(i_1=53°\)