Distance focale image
Partie
Question
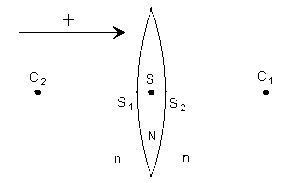
On réalise des lentilles minces possédant un centre de symétrie S à l'aide d'un verre d'indice absolu N = 1,5.
Quels modules devrait-on donner au rayon de courbure R de ces lentilles, pour obtenir, dans l'air, les distances focales suivantes : 1cm, 2cm, 4cm, 8cm, 16cm, 32cm, 64cm.
Exprimer le module de la vergence
Rappel de cours
Tout rayon passant par le centre optique d'une lentille mince n'est pas dévié.
Tout rayon incident parallèle à l'axe principal émerge de la lentille en passant par le foyer principal image.
Tout rayon incident passant par le foyer objet émerge de la lentille parallèlement à l'axe principal.
Pour une lentille sphérique mince, il existe deux plans focaux symétriques par rapport à la lentille: le plan focal objet et le plan focal image. Ces plans comme les foyers qui les forment sont réels pour une lentille convergente et virtuels pour une lentille divergente.
Une lentille mince est optiquement définie par sa distance focale.
Les relations de conjugaison :
origine au centre
\(-\frac1{\overline{OA}}+\frac1{\overline{OA'}}=\frac1{f'}\)
\(\gamma=\frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{OA'}}{\overline{OA}}=\frac{p'}p\)
origine aux foyers
\(\overline{FA}=x\) et \(\overline{F'A'}=x'\)
\(x\cdot x'=-f'^2\)
\(\gamma=\frac{f'}x=-\frac{x'}{f'}\)
Solution détaillée
Le module de la vergence \(|V|=|n/f'|\) d'une lentille mince en verre d'indice \(N\), immergée dans un milieu d'indice \(n = 1\), est :
\(\frac n{f'}=(N-n)\cdot\left(\frac1{R_1}-\frac1{R_2}\right)|V|=(N-1)\cdot\left|\left(\frac1{R_1}-\frac1{R_2}\right)\right|\)
\(\left|\frac1{f'}\right|=(N-1)\cdot\left|\left(\frac1{R_1}-\frac1{R_2}\right)\right|=(N-1)\cdot\left|\left(\frac2{R_1}\right)\right|=(N-1)\cdot\left|\left(\frac2{|R|}\right)\right|\)
La symétrie par rapport au centre \(( R_1 = - R_2 )\) et \(N = 1,5\) donne immédiatement \(f ' = R_1\) d'où: