Vergence et distance focale image
Partie
Question
Un fabricant de lentilles d'objectif pour appareil jetable utilise un moule de fabrication dont l'empreinte en creux sphérique de rayon \(R_1 = 8 \textrm{mm}\) détermine la courbure du dioptre d'entrée dans la lentille.
Quel est le signe de la distance focale image du dioptre d'entrée dans cette lentille ? L'axe repère est orienté positivement dans le sens de propagation de la lumière.
Sachant que ces lentilles minces sont en plastique d'indice moyen \(N = 1,5\) et de distance focale image \(f ' = 18 \textrm{mm}\), calculer le rayon \(R_2\) du dioptre de sortie de cette lentille ?
Utiliser la relation donnant la distance focale d'un dioptre sphérique.
Aide simple
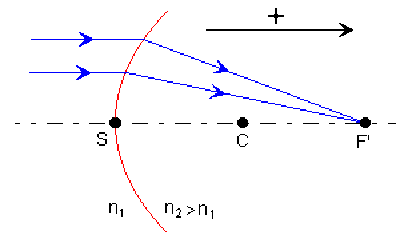
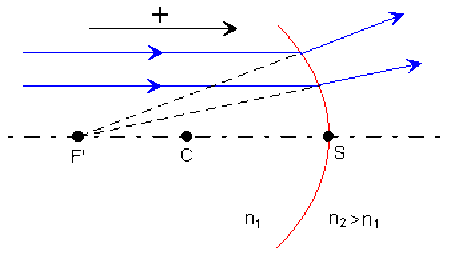
La distance focale image d'un dioptre sphérique de rayon \(R =\overline{SC}\) composé d'un milieu d'incidence (d'entrée) d'indice \(n_1\) et d'un milieu d'émergence (de sortie) d'indice \(n_2\) est : \(\overline{SF'}=f'=\frac{n_2}{n_2-n_1}\cdot\overline{SC}\)
Aide détaillée
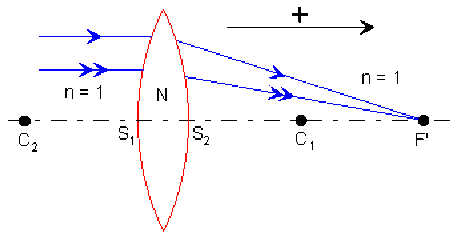
La distance focale image dans l'air \(f '\) d'une lentille mince de rayons \(\overline{S_1C_1}=R_1\) et \(\overline{S_2C_2}=R_2\) réalisée avec un milieu d'indice de réfraction moyen \(N\) est calculable par : \(\frac1{f'}=(N-1)\cdot\left(\frac1{R_1}-\frac1{R_2}\right)\)
Rappel de cours
Tout rayon passant par le centre optique d'une lentille mince n'est pas dévié.
Tout rayon incident parallèle à l'axe principal émerge de la lentille en passant par le foyer principal image.
Tout rayon incident passant par le foyer objet émerge de la lentille parallèlement à l'axe principal.
Pour une lentille sphérique mince, il existe deux plans focaux symétriques par rapport à la lentille: le plan focal objet et le plan focal image. Ces plans comme les foyers qui les forment sont réels pour une lentille convergente et virtuels pour une lentille divergente.
Une lentille mince est optiquement définie par sa distance focale.
Les relations de conjugaison :
origine au centre
\(-\frac1{\overline{OA}}+\frac1{\overline{OA'}}=\frac1{f'}\)
\(\gamma=\frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{OA'}}{\overline{OA}}=\frac{p'}p\)
origine aux foyers
\(\overline{FA}=x\) et \(\overline{F'A'}=x'\)
\(x\cdot x'=-f'^2\)
\(\gamma=\frac{f'}x=-\frac{x'}{f'}\)
Solution détaillée
Avec la convention d'orientation de l'axe, le dioptre d'entrée a un rayon \(\overline{S_1C_1}\) positif de même que \(N-1\) puisque \(N = c / v > 1\). Pour le dioptre sphérique étudié, le signe de :
\(f'=\left(\frac N{N-1}\right)\cdot\overline{S_1C_1}\), c'est-à-dire \(\frac{(>0)}{(>0)}\cdot(>0)\) est \(>0f'>0\)
Dans l'air d'indice \(n = 1\), la vergence \(\frac n{f'}=(N-n)\cdot\left(\frac1{R_1}-\frac1{R_2}\right)\) de cette lentille donne :
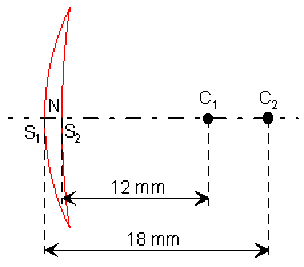
\(\frac1{f'}=(N-1)\cdot\left(\frac1{R_1}-\frac1{R_2}\right)\) ou \(\frac{N-1}{R_2}=\frac{N-1}{R_1}-\frac1{f'}\)
soit \(R_2=\frac{N-1}{\frac{N-1}{R_1}-\frac1{f'}}=\left(\frac{1}2\right)\cdot\left(\frac1{\frac1{12}-\frac1{18}}\right)=18 \textrm{mm}\)
\(R_2=18\textrm{mm}\)