L'objectif
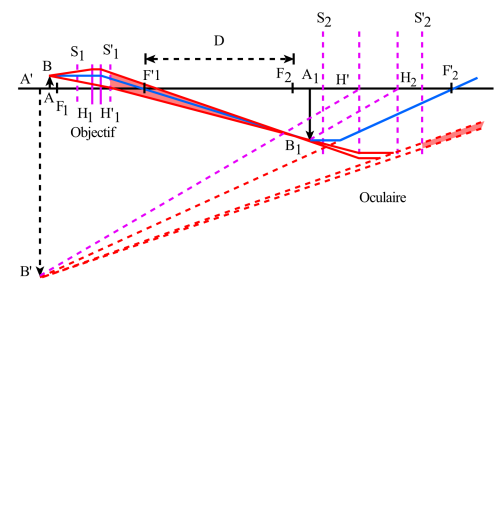
L'objectif est un système épais convergent[1] de faible distance focale[2] \(F_{\mathit1}\). L'objet \(AB\) est placé un peu au delà du foyer objet[3] \(F_{\mathit1}\) et l'objectif en donne une image réelle[4] \(A_{\mathit1}B_{\mathit1}~\), \(~\gamma_{\mathit1}\) fois plus grande que l'objet[5].
La distance \(F'_{\mathit1}F_{\mathit2}\) du foyer image[3] de l'objectif au foyer objet de l'oculaire est appelé intervalle optique du microscope ; elle est constante et est normalisée à 16 cm. Le grandissement[6] propre de l'objectif est donné pour : \(~\overline{F'_{\mathit1}A_{\mathit1}}=\Delta~\) et l'on obtient en valeur absolue : \(~|\gamma_{\mathit1}|=\frac{\Delta}{|f_{\mathit1}|}\)
L'image \(A_{\mathit1}B_{\mathit1}\) donnée par l'objectif et l'image virtuelle[7] \(A'B'\) donnée par le microscope sont toujours située dans l'air par contre l'objet \(AB\) pourrait être situé dans un milieu[8] d'indice \(n\).
L'objectif travaille à grande ouverture[9] dans espace objet[10] et la condition d'aplanétisme[11] est réalisée pour les points \(A\) et \(A_{\mathit1}\).
Nous avons alors : \(n~.~AB~.~\sin~u=A_{\mathit1}B_{\mathit1}~.~\sin~u_{\mathit1}\)
Comme, grâce aux différentes lentilles constituant l'objectif qui réduisent progressivement l'ouverture des faisceaux, on peut considérer que le faisceau[1] utile est paraxial, on peut écrire :
\(n~.~AB~.~\sin~u=A_{\mathit1}B_{\mathit1}~.~u_{\mathit1}~\) et \(~\gamma_{\mathit1}=\frac{n~.~\sin~u}{u_{\mathit1}}=\frac{O_n}{u_{\mathit1}}\)
\(O_n\) est appelée ouverture numérique de l'objectif.