Les éléments cardinaux
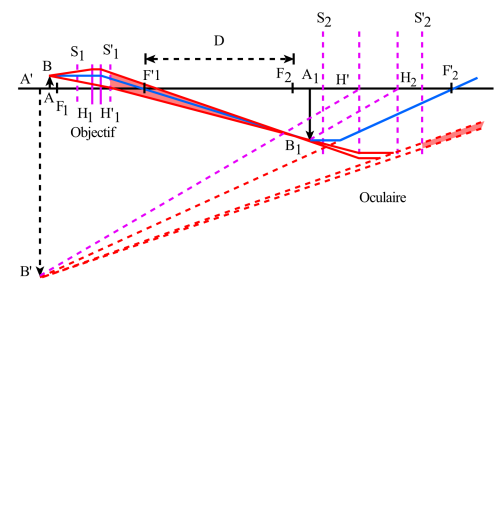
La distance focale[1] image du microscope est : \(~f'=\overline{H'F'}=\frac{f_{\mathit1}~.~f'_{\mathit2}}{\Delta}<0~\) et elle est négative : le microscope est un système divergent[2].
Appliquons les formules de Newton :
\(\overline{F_{\mathit1}F}~.~\overline{F'_{\mathit1}F_{\mathit2}}=-f_{\mathit1}^2~~\) \(~~\overline{F_{\mathit1}F}=-\frac{f_{\mathit1}^2}{\Delta}<0\)
\(\overline{F_{\mathit2}F'_{\mathit1}}~.~\overline{F'_{\mathit2}F'}=-f_{\mathit2}^2~~\) \(~~\overline{F'_{\mathit2}F'}=\frac{f_{\mathit2}^2}{\Delta}>0\)
si nous reprenons les valeurs numériques pour un microscope type nous obtenons :
\(f'=\frac{5,4~.~17}{160}=0,57~\mathrm{mm}~\) et \(~\overline{F_{\mathit1}F}=-\frac{5,4^2}{160}=-0,18~\mathrm{mm}\)
On constate que la distance focale du microscope est très faible et que les foyers \(F\) et \(F'\) du microscope sont très voisins des foyers extérieurs \(F_{\mathit1}\) de l'objectif et \(F'_{\mathit2}\) de l'oculaire.