Le cercle oculaire
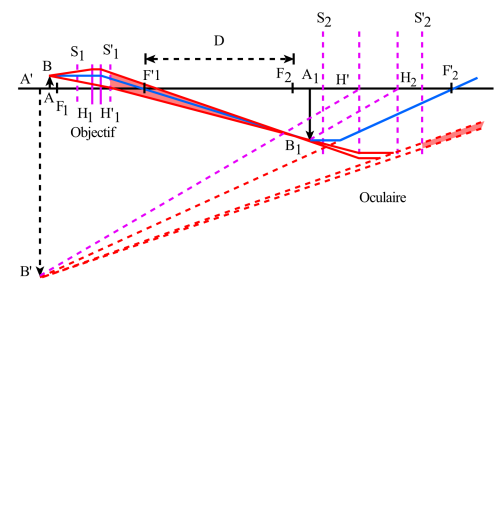
La pupille de sortie du microscope ou cercle oculaire joue un rôle important puisque c'est dans son plan que doit être placée la pupille de l'oeil pour recevoir le maximum de lumière de l'instrument.
Les lentilles qui constituent l'objectif ont des diamètres très faibles par rapport à la longueur du microscope et le diaphragme d'ouverture est souvent défini par le diamètre de la première lentille de l'objectif et sa distance au foyer objet[1] de l'oculaire est assez peu différente de \(\Delta\). Le cercle oculaire n'est alors que l'image[2] de ce diaphragme à travers tout le système optique[3] postérieur et en appliquant la formule de Newton ( si \(C'\) est le centre du cercle oculaire ou point oculaire) :
\(\overline{F'_{\mathit2}C'}\approx\frac{f_{\mathit2}^2}{\Delta}=\overline{F'_{\mathit2}F'}\)
On voit que le point oculaire \(C'\), le foyer image[1] \(F\)' du microscope et le foyer image \(F'_{\mathit2}\) de l'oculaire sont pratiquement confondus.
Comme on devra placer le centre optique[4] de l'oeil en ce point les puissances[5] \(P\) et \(P_{\mathit2}\) du microscope et de l'oculaire seront des puissances intrinsèques et on aura : \(~P=\frac1f~\) et \(~P_{\mathit2}=\frac1{f_{\mathit2}}~\)
Si l'on appelle \(R\) le rayon du diaphragme d'ouverture et \(R'\) le rayon du cercle oculaire nous avons suivant la formule de Newton : \(~R'=R~.~\frac{f_{\mathit2}}{\Delta}\)
si nous reprenons l'exemple de notre microscope type avec R = 3 mm : \(~R'= 0,1.R = 0,3~\mathrm{mm}\).
Le rayon du cercle oculaire est très petit et pratiquement toujours inférieur au rayon de la pupille de l'oeil.
(Ceci entraîne une limitation de la luminosité.)