Description schématique [Lunette astronomique]

Description schématique

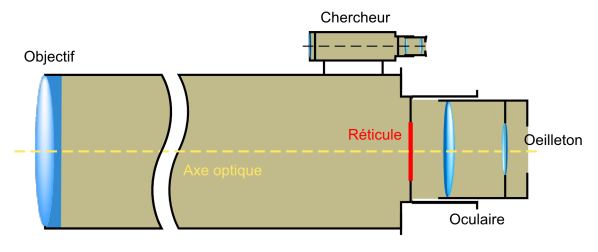
Une lunette astronomique comporte deux systèmes centrés dont l'axe commun est l'axe de la lunette.

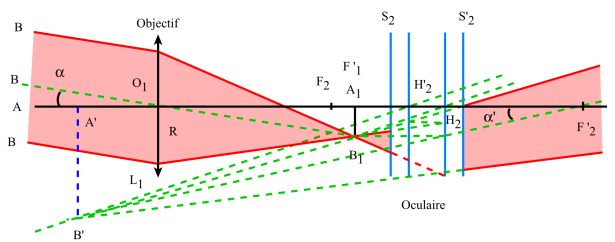
Etudions dans le cas d'un oculaire positif, le cheminement d'un faisceau^[1] issu du bord supérieur B d'un astre de diamètre apparent \(\alpha\), le bord inférieur A étant suivant l'axe de la lunette.

L'objectif est un système convergent^[1] constitué par plusieurs lentilles que nous assimilerons à une lentille mince^[2] \(L_{\mathit1}\) de distance focale^[3] \(f_{\mathit1}\) grande (plusieurs mètres) et d'ouverture relative 2 R / f1 (de l'ordre de 1/20 à 1/10).

L'objectif donne de l'objet \(AB\) une image réelle^[4] \(~A_{\mathit1}B_{\mathit1}~\) dans son plan focal image \(F'_{\mathit1}\). L'objet \(AB\) étant très éloigné et si \(\alpha\) est son diamètre apparent l'image^[5] donnée par l'objectif a pour dimension : \(~A_{\mathit1}B_{\mathit1}=\alpha.f_{\mathit1}~\) et elle est renversée par rapport à l'objet^[6].

Cette image est observée à travers un oculaire (constitué le plus souvent par un doublet de type Ramsden ou Huyghens) et l'image objective joue alors le rôle d'objet virtuel^[7] pour la lentille de champ de l'oculaire. Cet oculaire a une distance focale \(f_{\mathit2}\) qui peut varier entre 4 cm et 1 cm.

L'image objective \(A_{\mathit1}B_{\mathit1}\) doit se trouver entre le foyer \(F_{\mathit2}\) de l'oculaire et le plan principal objet \(H_{\mathit2}\) de l'oculaire. Lorsque \(A_{\mathit1}B_{\mathit1}\) se trouve en \(F_{\mathit2}\), c'est-à-dire lorsque le foyer image^[8] de l'objectif \(F'_{\mathit1}\) et le foyer objet^[8] de l'oculaire \(F_{\mathit2}\) sont confondus, l'image finale \(A'B'\) est rejetée à l'infini ; on dit alors que la lunette est afocale et le grandissement^[9] est alors donné par le rapport des focales \(~f_{\mathit1}~\) et \(~f_{\mathit2}~\) : \(~\gamma=\frac{f_{\mathit2}}{f_{\mathit1}}\)

Pour mettre au point l'observateur devra amener l'image \(A'B'\) dans ses limites de vision distincte en déplaçant l'oculaire par rapport à l'objectif et sa latitude de mise au point sera typiquement de l'ordre de quelques mm, c'est pourquoi une vis micrométrique n'est pas nécessaire pour déplacer l'oculaire par rapport à l'objectif : une vis à crémaillère suffira.

Simuler

L'animation suivante permet d'observer la marche des rayons au travers d'une lunette :

La lunette

Notes

Faisceau Lumineux
Un faisceau lumineux est constitué d'un ensemble de rayons.
Il peut être :
- parallèle si les rayons qui le constituent sont parallèles,
- convergent si les rayons qui le constituent, convergent vers un même point
- divergent si les rayons qui le constituent, semblent provenir d'un même point.
Remarque :
Un faisceau convergent devient un faisceau divergent après passage par le point de convergence.
Lentille mince
Une lentille dont l'épaisseur au centre optique est négligeable devant les rayons de courbure des dioptres qui la limitent est dite mince. Dans le cas contraire c'est une lentille épaisse.
Approximation des lentilles minces
Une lentille mince peut être représentée par une lentille infiniment mince lorsqu'on étudie ses propriétés pour des distances [lentille-objet] ou [lentille-image] grandes devant l'épaisseur de la lentille. C'est ce qui est fait dans le cadre de l'optique géométrique élémentaire et en particulier dans l'atelier-schéma.
Distance focale d'une lentille
C'est la mesure algébrique de OF' où O est le centre optique et F' le foyer principal image.
Elle est positive pour une lentille convergente.
Puissance intrinseque (ou vergence) d'une lentille
C'est l'inverse de la distance focale exprimée en mètres, elle s'exprime en dioptries.
La puissance intrinseque d'une loupe de (distance) focale 5 cm est de 20 dioptries.
Image Réelle
Une image réelle se forme au delà de la face de sortie du système optique, dans l'espace image réelle.
Les rayons issus du point objet conjugué y convergent.
L'image réelle peut être observée directement ou bien recueillie sur un écran.
Lorsqu'on utilise un écran, c'est la lumière diffusée par l'écran qui parvient à notre oeil et non pas les rayons lumineux issus de l'objet.
Au cinéma, ce sont des images réelles que l'on observe sur l'écran.
Lorsqu'on prend une photo, l'image renversée qui se forme dans le plan de la pellicule, est une image réelle.
Image
On appelle image d'un objet par un système optique, l'ensemble des images des points de l'objet.
On appelle image d'un point, la zone de convergence des rayons, après traversée du système optique (image réelle) ou la zone d'où les rayons semblent provenir (image virtuelle). Lorsque cette zone se réduit à un point, le système est dit stigmatique.
En pratique, l'image ressemble à l'objet (sinon le système ne présente pas d'intérêt), elle peut être
- agrandie : plus grande que l'objet ( |grandissement| >1) ;
- rapetissée : plus petite que l'objet ( |grandissement| <1) ;
- droite : dans le même sens que l'objet (grandissement >0) ;
- renversée : dans le sens contraire à l'objet (grandissement <0) ;
- déformée : un système qui déforme parce qu'il n'a pas le même grandissement dans différentes directions provoque une anamorphose (ex : glace déformante) ;
- floue
Objet
En optique, on appelle objet tout ensemble de points lumineux. Il peut s'agir d'une source primaire qui produit de la lumière (ex : soleil, étoiles, filament de lampe allumée, écran de télévision ou d'ordinateur en fonction), ou d'une source secondaire qui diffuse une partie de la lumière qu'elle reçoit (ex : lune, planètes, la plupart des objets qui nous entourent lorsqu'ils sont éclairés).
On considère, en général, des objets plans situés dans des plans de front de systèmes optiques.
Dans des systèmes composés on pourra considérer qu'une image produite par une première partie du système est un objet pour le reste du système.
Objet Virtuel
Un objet virtuel est un ensemble de points définis par la convergence du prolongement de rayons. Il est situé après la face d'entrée du système optique, dans l'espace objet virtuel.
La convergence des rayons qui définissent un tel objet n'aurait réellement lieu qu'en l'absence du système optique.
Dans un système optique composé, une image réelle, formée par une première partie du système, peut être considéré comme un objet virtuel pour la seconde partie si l'image en question est située au delà de cette seconde partie.
Foyers
Un foyer image est le point où convergent, après traversée du système optique, les rayons d'un faisceau parallèle. Il est dit principal sur l'axe principal, et secondaire en dehors de cet axe.
Un foyer objet est le point d'où partent les rayons qui, après traversée du système optique, forment un faisceau parallèle. Il est dit principal sur l'axe principal, et secondaire en dehors de cet axe.
Dans l'approximation des lentilles minces, l'ensemble des foyers secondaires et le foyer principal sont tous situés dans un plan de front appelé plan focal.
Grandissement
Le grandissement est un nombre algébrique, rapport entre les dimensions de l'image \(A'B'\) et de l'objet \(AB\) :
\(\gamma=\frac{\overline{A'B'}}{\overline{AB}}\)
Lorsque le système est aplanétique, l'image \(A'B'\) d'un objet \(AB\) situé dans un plan de front est également dans un plan de front. Le grandissement mesuré dans ces conditions est un grandissement transverse.
Le grandissement longitudinal (ou axial) est le rapport algébrique des dimensions de l'image et de l'objet prises suivant l'axe principal du système optique.
Le grandissement, parfois appelé grandissement linéaire ne doit pas être confondu avec le grossissement \(G\) qui fait référence à des angles.