Lunette astronomique

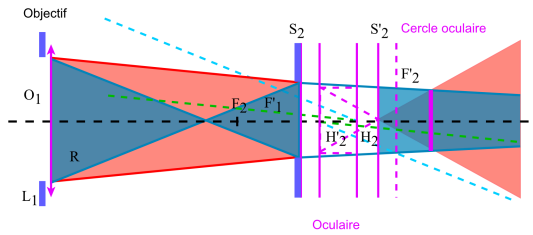
La face d'entrée de l'objectif constitue le diaphragme d'ouverture de l'instrument et la pupille de sortie ou cercle oculaire est l'image^[1] de la monture de l'objectif à travers l'oculaire. Il faudra donc placer la pupille de l'oeil dans le plan du cercle oculaire de manière à ce que l'oeil reçoive le flux lumineux maximum ; un oeilleton à la sortie de l'oculaire permet d'y placer l'oeil à cet effet.

Si \(C'\) est le centre du cercle oculaire, en appliquant la formule de Newton on a :

\(\overline{F'_{\mathit2}C'}=-\frac{f_{\mathit2}^2}{\overline{F_{\mathit2}O_{\mathit2}}}=-\frac{f_{\mathit2}^2}{\overline{F_{\mathit2}F'_{\mathit1}}~+~\overline{F'_{\mathit1}O_{\mathit2}}}\approx\frac{f_{\mathit2}^2}{f_{\mathit1}}=\frac{f_{\mathit2}}{f_{\mathit1}}~.~f_{\mathit2}\)

Comme \(f_{\mathit2}/f_{\mathit1}\) est petit devant 1, \(F'_{\mathit2}C'\) sera petit devant \(f_{\mathit2}\). On en déduit donc que le cercle oculaire est au delà mais très près du plan focal image de l'oculaire.

On pourra alors confondre le plan du cercle oculaire avec le plan focal image de l'oculaire et le plan de la pupille de l'oeil. Le diamètre O' du cercle oculaire est donné par :

\(O'=\frac{R'}R=\frac{F'_{\mathit2}C'}{f_{\mathit1}}\approx\frac{f_{\mathit2}}{f_{\mathit1}}\)

soit : \(O'=O~.~\frac{f_{\mathit2}}{f_{\mathit1}}\)

le diamètre du cercle oculaire d'une lunette astronomique est en général inférieur au diamètre de la pupille de l'oeil.

Le grossissement^[2] de la lunette est donné par :

\(G=\frac{\alpha'}{\alpha}=f_{\mathit1}~.~P_{\mathit2}=\frac{P_{\mathit2}}{P_{\mathit1}}\)

c'est à dire le produit de la distance focale^[3] (en mètres) de l'objectif par la puissance^[3] (en dioptries) de l'oculaire.

Dans le cas d'une lunette afocale la puissance de l'oculaire est sa puissance intrinsèque et l'on a rigoureusement :

\(G=\frac{f_{\mathit1}}{f_{\mathit2}}=\frac R{R'}=\frac O{O'}\)

Si la pupille de l'oeil est dans le plan focal image de l'oculaire c'est-à-dire dans le plan du cercle oculaire la puissance de l'oculaire est encore sa puissance intrinsèque et la formule précédente du grossissement^[2] est encore valable. Cette relation donne le grossissement intrinsèque de la lunette.

L'animation suivante permet d'observer la marche des rayons au travers d'une lunette :