Projection orthogonale d'un vecteur sur un axe
Définition :
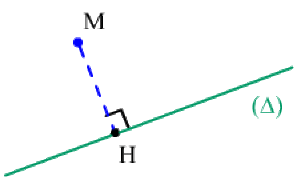
On appelle projection orthogonale d'un point \(M\) sur un axe \((\Delta)\) ,
le point \(H\), intersection de la perpendiculaire à \((\Delta)\) passant par \(M\) avec la droite \((\Delta)\).
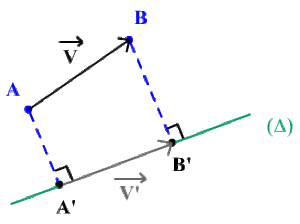
La projection orthogonale d'un vecteur \(\overrightarrow{V}\) (représenté par \(\overrightarrow{AB}\)) sur un axe \((\Delta)\) est un vecteur \(\overrightarrow{V'}\) (représenté par \(\overrightarrow{A'B'}\)) appartenant à \((\Delta)\) d'origine \(A'\) et d'extrémité \(B'\).
Les points \(A'\) et \(B'\) sont les points projetés orthogonalement sur \((\Delta)\) des points \(A\) et \(B\).
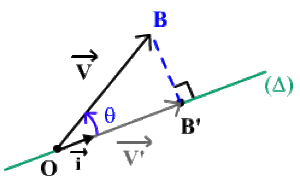
Cas particulier : l'origine du vecteur \(\overrightarrow{V}\) se trouve sur l'axe \((\Delta)\).
Soit \(\overrightarrow{OB}\) un représentant de \(\overrightarrow{V}\) et notons \(B'\) la projection orthogonale de \(B\) sur \((\Delta)\).
La mesure algébrique de \(\overrightarrow{OB'}\), représentant de \(\overrightarrow{V'}\), est :
\(\overrightarrow{OB'} = \Arrowvert\overrightarrow{OB'} \Arrowvert \cos \theta ~\textrm{ où }~ \theta = \Big(\overrightarrow{OB'},\overrightarrow{OB} \Big)\)
\(\overrightarrow{OB'} > 0\) pour \(0<\theta<\frac{\pi}{2}\) ;\(\overrightarrow{OB'} = 0\) pour \(\theta = \frac{\pi}{2}\) ; \(\overrightarrow{OB'}<0\) pour \(\frac{\pi}{2} < \theta < \pi\)
Propriété :
Si \(\overrightarrow{U} = \overrightarrow{V}\) alors \(\textrm{proj }\overrightarrow{U} = \textrm{proj } \overrightarrow{V}\)
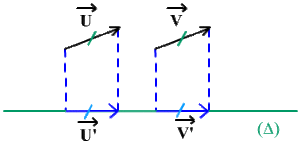
\(\textrm{proj }\Big(\overrightarrow{U} + \overrightarrow{V} \Big) = \textrm{proj }\overrightarrow{U} + \textrm{proj }\overrightarrow{V}\)
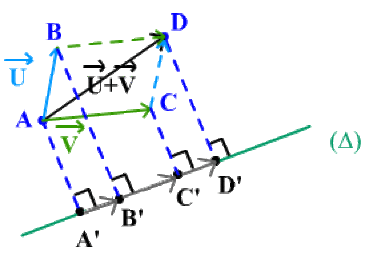
\(\textrm{proj }\Big(\overrightarrow{U} + \overrightarrow{V} \Big) = \textrm{proj }\overrightarrow{AD} = \overrightarrow{A'D'} = \overrightarrow{A'B'} + \overrightarrow{A'C'} = \textrm{proj }\overrightarrow{U} + \textrm{proj }\overrightarrow{V}\)
\(\textrm{proj }\Big(\alpha \overrightarrow{U} \Big) = \alpha ~\textrm{proj }\overrightarrow{U}\)
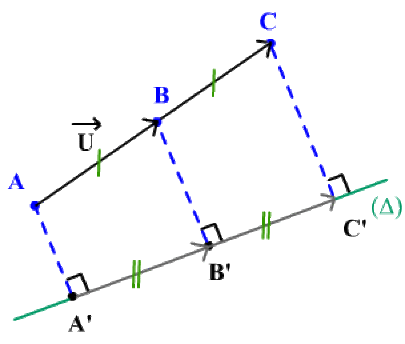
\(\overrightarrow{AC} = \alpha \overrightarrow{AB} = \alpha \overrightarrow{V}\) \((\alpha = 2)\)
\(\textrm{proj }\Big(\alpha \overrightarrow{U}\Big) = \textrm{proj }\overrightarrow{AC}= \overrightarrow{A'C'} = \alpha~ \overrightarrow{A'B'} = \alpha~\textrm{proj }\overrightarrow{AB} = \alpha~\textrm{proj }\overrightarrow{U}\)
Applications
Exemple : Matrice de projection
Matrice de projection orthogonale:
Soit \(P\) la projection orthogonale sur un plan \(xOy\).
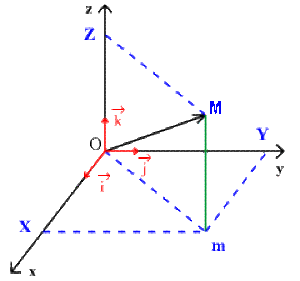
\(\mathcal{P}~\Big(\vec{i}\Big) = \vec{i}\) ; \(\mathcal{P}~\Big(\vec{j}\Big) = \vec{j}\) ; \(\mathcal{P}~\Big(\vec{k}\Big) =\overrightarrow{0}\)
On construit la matrice \(P\) de la projection orthogonale de la base \(\Big(\vec{i},\vec{j},\vec{k} \Big)\) dans la base \(\Big(\vec{i},\vec{j} \Big)\) par :
\(\begin{array}{ll}\vec{i} \\ \\ \vec{j} \end{array}\overset{\begin{array}{l}\mathcal{P}\Big(\vec{i}\Big)~ \mathcal{P}\Big(\vec{j}\Big)~ \mathcal{P}\Big(\vec{k}\Big) \end{array}}{\left(\begin{array}{rcccccl} 1 && 0 && 0 \\ \\ 0 && 1 && 0 \end{array}\right)}\)
Pour un vecteur \(\overrightarrow{OM} = X\vec{i} + Y\vec{j} + Z\vec{k}\) ou \(\overrightarrow{OM} = \left(\begin{array}{c} X \\ Y \\ Z \end{array}\right)\) dans la base \(\Big(\vec{i},\vec{j},\vec{k} \Big)\), la projection sur le plan \(xOy\) s'obtient par :
\(\overrightarrow{Om} = \mathcal{P} \Big(\overrightarrow{OM} \Big) \Leftrightarrow \left(\begin{array}{rcl} 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right) \left(\begin{array}{c} X \\ Y \\ Z \end{array}\right) = \left(\begin{array}{c} X \\ Y \end{array}\right)\)
\(\overrightarrow{Om} = X \vec{i} + Y \vec{j}\)
(Voir le chapitre "Calcul matriciel" : Produit de deux matrices)
Exemple : Le pendule conique
Une masse \(m\), attachée à un fil de longueur \(l\) est en rotation à une vitesse angulaire \(\omega\) constante sur une circonférence de rayon \(r = l \sin \theta\).
Déterminer la valeur de l'angle \(\theta\) en fonction de \(l\), \(\omega\) et \(g\) (\(g\) : accélération de la pesanteur).
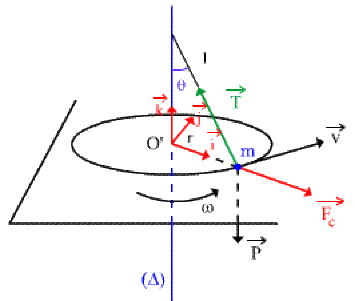
Les trois forces ( \(\overrightarrow{P}\) : poids, \(\overrightarrow{T}\): tension, \(\overrightarrow{F_{c}}\): force centrifuge) déterminent l'équilibre relatif de la masse m dans la base \(\Big(\vec{i},\vec{j},\vec{k} \Big)\)
\(\overrightarrow{P} + \overrightarrow{T} + \overrightarrow{F_{c}} = \overrightarrow{0}\)
Par projection orthogonale de cette relation d'équilibre :
\(\left. \begin{array}{ll} \textrm{sur }\vec{i} : \quad -T \sin\theta + F_{c} = 0 \\\textrm{sur }\vec{k} : \quad +T \cos \theta - P = 0 \end{array} \right\} \quad \tan \theta = \frac{F_{c}}{P}\)
avec \(P = mg\)
et \(F_{c} = m \gamma_{c} = mr\omega^{2} = ml ~\sin \theta ~\omega^{2}\)
d'où \(\tan \theta = \frac{ml~\omega^{2} \sin{\theta}}{mg}\)
\(\cos \theta = \frac{g}{l\omega^{2}}\)