Applications
Circuit R, L, C série en courant alternatif sinusoïdal : construction de Fresnel
Soit le circuit série \(R, L, C\) traversé par un courant \(i(t) = I_m \cos \omega t\)
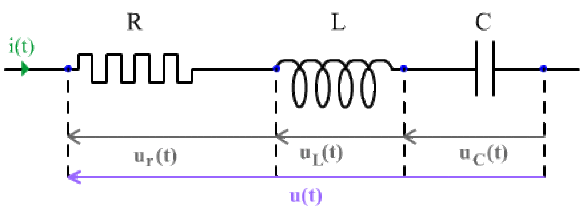
La différence de potentiel \(u(t) = U_m \cos(\omega t + \varphi)\) aux bornes de l'ensemble est la somme des d.d.p. instantanées aux bornes de chaque dipôle :
\(u(t) = u_r(t) + u_L(t) + u_C(t)\)
avec
\(u_r(t) = RI_m \cos \omega t\)
\(u_{L}(t) = L ~\frac{di(t)}{dt} = -L \omega I_{m} \sin \omega t = L \omega I_{m} \cos\Big(\omega t + \frac{\pi}{2} \Big)\)
\(u_{C}(t) = \frac{1}{C} \int i(t) dt = \frac{1}{C \omega} I_{m} \sin \omega t = \frac{1}{C \omega} I_{m} \cos \Big(\omega t - \frac{\pi}{2} \Big)\)
Représentation de Fresnel : Associons à :
la tension \(u_r(t)\) le vecteur tournant \(\overrightarrow{OM_{1}}\)
\(\Big \Arrowvert \overrightarrow{OM_{1}} \Big \Arrowvert = RI_{m}\) ; \(\Big(\overrightarrow{Ox}, \overrightarrow{OM_{1}} \Big) = \omega t\) ; \(\overrightarrow{Om_{1}} = RI_{m} \cos \omega t = u_{r}(t)\)
la tension \(u_L(t)\) le vecteur tournant \(\overrightarrow{OM_{2}}\)
\(\Big \Arrowvert \overrightarrow{OM_{2}} \Big \Arrowvert = L \omega ~I_{m}\) ; \(\Big(\overrightarrow{Ox}, \overrightarrow{OM_{2}} \Big) = \omega t + \frac{\pi}{2}\) ; \(\overrightarrow{Om_{2}} = L \omega~ I_{m} \cos \Big(\omega t + \frac{\pi}{2} \Big)= u_{L}(t)\)
la tension \(u_C(t)\) le vecteur tournant \(\overrightarrow{OM_{3}}\)
\(\Big \Arrowvert \overrightarrow{OM_{3}} \Big \Arrowvert = \frac{I_{m}}{C \omega}\) ; \(\Big(\overrightarrow{Ox}, \overrightarrow{OM_{3}} \Big) = \omega t - \frac{\pi}{2}\) ; \(\overrightarrow{Om_{3}} = \frac{I_{m}}{C \omega}\cos \Big( \omega t - \frac{\pi}{2} \Big)= u_{C}(t)\)
la tension aux bornes de l'ensemble \(u(t) = u_R(t) + u_L(t) + u_C(t)\) associée au vecteur tournant \(\overrightarrow{OM} = \overrightarrow{OM_{1}} + \overrightarrow{OM_{2}} + \overrightarrow{OM_{3}}\) est représentée ci-dessous aux instants \(t \ne 0\) et \(t = 0\).
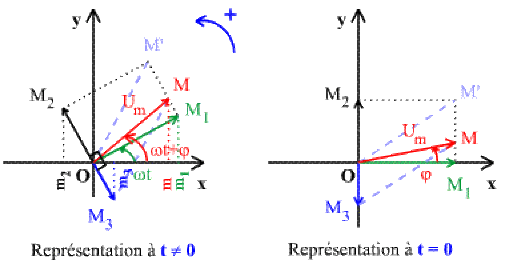
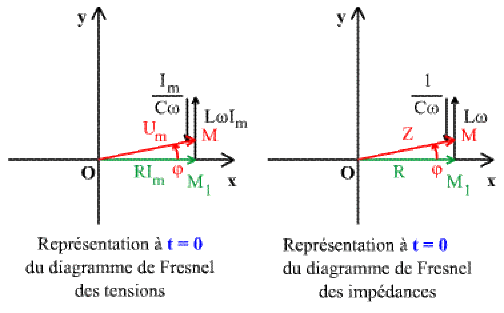
Dans le triangle \(OM_{1}M\), nous avons : \({\overline{OM}}^{2} = {\overline{OM_{1}}}^{2} + {\overline{M_{1}M}}^{2}\) d'où
Module de \(u(t)\) :
\(U_{m} = \sqrt{(RI_{m})^{2} + \Big(L \omega I_{m} - \frac{I_{m}}{C\omega} \Big)^{2}} = I_{m} \sqrt{R^{2} + \Big(L \omega - \frac{1}{C\omega}\Big)^{2}}\)
Argument de \(u(t)\) par rapport à \(i(t)\) :
\(\tan \varphi =\frac{M_{1}M}{OM_{1}} \Rightarrow \varphi = \textrm{Arctan }\frac{L \omega - 1/C \omega}{R}\)
Composition de deux mouvements vibratoires sinusoïdaux. Interférences : construction de Fresnel
Un diapason permet de créer à la surface d'un liquide deux sources synchrones \(S_1\) et \(S_2\) vibrant selon la loi:
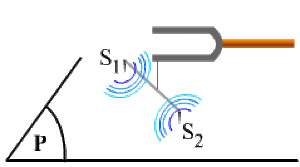
\(s_{1}(t) = s_{2}(t) = S_{0} \cos \omega t = S_{0} \cos 2 \pi \frac{t}{T}\)
Un point \(M\) de la surface du liquide reçoit :
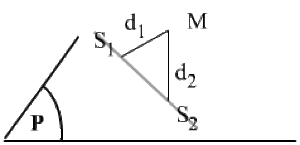
de \(S_1\) à la distance \(d_1\) une vibration :
\(s_{1M}(t) = S_{0} \cos 2 \pi \Big(\frac{t}{T} - \frac{d_{1}}{\lambda} \Big) = S_{0} \cos (\omega t - \varphi_{1})\) avec \(\varphi_{1} = \frac{2 \pi d_{1}}{\lambda}\)
avec \(\lambda\), longueur d'onde \(\lambda = VT = V/N\)
de \(S_2\) à la distance \(d_2\) une vibration :
\(s_{2M}(t) = S_{0} \cos 2 \pi \Big(\frac{t}{T} - \frac{d_{2}}{\lambda} \Big) = S_{0} \cos (\omega t - \varphi_{2})\) avec \(\varphi_{2} = \frac{2 \pi d_{2}}{\lambda}\)
La vibration résultante en \(M\) est donc (dans le cas des petites déformations) : \(s_M(t) = s_{1M}(t) + s_{2M}(t)\)
Construction de Fresnel : Associons à :
la vibration \(s_{1M}(t) = S_0 \cos(\omega t - \varphi_1)\) le vecteur tournant \(\overrightarrow{OM_{1}}\)
la vibration \(s_{2M}(t) = S_0 \cos(\omega t - \varphi_2)\) le vecteur tournant \(\overrightarrow{OM_{2}}\)
la vibration résultante \(s_M(t) = s_{1M}(t) + s_{2M}(t)\) le vecteur tournant \(\overrightarrow{OM} = \overrightarrow{OM_{1}} + \overrightarrow{OM_{2}}\)
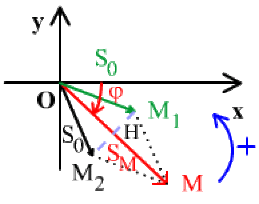
La figure \(OM_1MM_2\) est un losange car \(\Big \Arrowvert \overrightarrow{OM_{1}} \Big \Arrowvert = \Big \Arrowvert \overrightarrow{OM_{2}} \Big \Arrowvert = S_{0}\) nous avons :
l'amplitude
\(S_{M} = \Big \Arrowvert \overrightarrow{OM} \Big \Arrowvert = 2 \Big \Arrowvert \overrightarrow{OH} \Big \Arrowvert = 2 S_{0} \cos \frac{\varphi_{2} - \varphi_{1}}{2}\)
\(S_{M} = 2 S_{0} \cos \frac{\pi(d_{1} - d_{2})}{\lambda}\)
l'angle
\(\varphi = \frac{\varphi_{1} + \varphi_{2}}{2} = - \pi \frac{d_{1} + d_{2}}{\lambda}\)
d'où
\(\begin{array}{ll}s_{M}(t) &= 2 S_{M} \cos(\omega t + \varphi) \\ &= 2 S_{0} \cos \frac{\pi(d_{1} - d_{2})}{\lambda} \cos \Bigg(\omega t - \pi \frac{d_{1} + d_{2}}{\lambda} \Bigg) \end{array}\)
Franges de vibration maximum
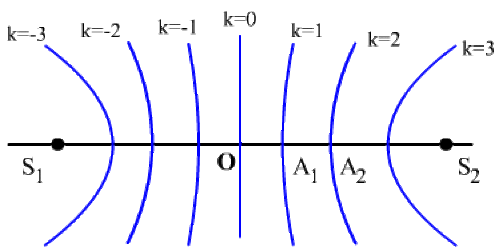
\(OA_{1} = A_{1}A_{2} = ... = \lambda/2\)
\(\Bigg \arrowvert \cos \frac{\pi(d_1 - d_2)}{\lambda}\Bigg \arrowvert = 1 \Leftrightarrow \pi \frac{d_1 - d_2}{\lambda} = k \pi \qquad k \in \mathbb{Z}\)
et \(d_1 - d_2 = k \lambda\), une famille d'hyperboles de foyers \(S_1\) et \(S_2\)
Franges de vibration nulle
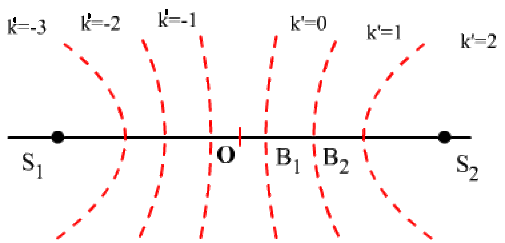
\(B_1B_2 = B_2B_3 = ... = \lambda/2\)
\(\cos \frac{\pi(d_1 - d_2)}{\lambda} = 0 \Leftrightarrow \pi \frac{d_1 - d_2}{\lambda} = \frac{\pi}{2} + k' \pi \qquad k' \in \mathbb{Z}\)
et \(d_1 - d_2 = (2k' + 1) \frac{\lambda}{2}\), une famille d'hyperboles de foyers \(S_1\) et \(S_2\)