Question 1
Durée : 4 mn
Note maximale : 6
Question
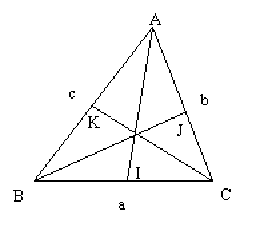
Soit \(a\), \(b\), \(c\) la longueur des côtés d'un triangle \(ABC\); \(I\), \(J\) et \(K\) les milieux respectifs des segments \(BC\), \(AC\), \(AB\);
\(\hat{A}\), \(\hat{B}\) et \(\hat{C}\) les angles intérieurs aux sommets du triangle \(ABC\).
Par utilisation de la relation de Chasles, démontrer la relation : \(a^{2} = b^{2} + c^{2} - 2bc \cos \hat{A}\)
En déduire les autres relations exprimant \(b\) et \(c\) en fonction de \(\hat{B}\) et \(\hat{C}\).
Solution
La relation de Chasles permet d'écrire \(\overrightarrow{BC} = \overrightarrow{BA} + \overrightarrow{AC}\) donc
\(\begin{array}{ll}{\overrightarrow{BC}}^{2} &= \overrightarrow{BC} . \overrightarrow{BC} \\ & = \left(\overrightarrow{BA} + \overrightarrow{AC}\right) . \left(\overrightarrow{BA} + \overrightarrow{AC} \right) \\ &= {\overrightarrow{BA}}^{2} + {\overrightarrow{AC}}^{2} + 2 \overrightarrow{BA} \cdot \overrightarrow{AC} \end{array}\)
avec \(\left(\overrightarrow{BA} ,\overrightarrow{AC}\right) = \pi - \hat{A}\)
et \(a^{2} = b^{2} + c^{2} + 2bc \cos \left( \pi - \hat{A}\right)\)
\(a^{2} = b^{2} + c^{2} - 2bc \cos \hat{A}\) ( 4 points )
et par analogie
\(\begin{array}{l} b^{2} = a^{2} + c^{2} - 2ac \cos \hat{B} \\ \\ c^{2} = a^{2} + b^{2} - 2ab \cos \hat{C} \end{array}\) ( 1 + 1 point )