Question 3
Durée : 7 mn
Note maximale : 8
Question
En déduire que la somme des carrés des longueurs des médianes du triangle est égale aux \(3/4\) de la somme des carrés des longueurs des côtés du triangle.
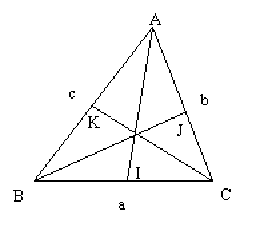
Solution
Par élévation au carré de la relation précédente nous avons :
\(4 ~{\overrightarrow{AI}}^{2} = \left(\overrightarrow{AB} + \overrightarrow{AC}\right)^{2}\)
\(= {\overrightarrow{AB}}^{2} + {\overrightarrow{AC}}^{2} + 2 \overrightarrow{AB} \cdot \overrightarrow{AC} = c^{2} + b^{2} + 2bc \cos \hat{A}\) ( 4 points )
sachant que \(a^{2} = b^{2} + c^{2} - 2bc \cos \hat{A}\) on en déduit :
\(\begin{array}{ll} 4 {AI}^{2} & = c^{2} + b^{2} + (b^{2} + c^{2} - a^{2}) \\ & = 2 b^{2} + 2c^{2} - a^{2} \end{array}\)
Des relations analogues pour les autres médianes conduisent à :
\(\begin{array}{ll} 4 {BJ}^{2} & = c^{2} + a^{2} + (c^{2} + a^{2} - b^{2}) \\ & = 2 a^{2} + 2c^{2} - b^{2} \end{array}\)
\(\begin{array}{ll} 4 {CK}^{2} & = a^{2} + b^{2} + (a^{2} + b^{2} - c^{2}) \\ & = 2 a^{2} + 2b^{2} - c^{2} \end{array}\)
d'où
\(4 \left({AI}^{2} + {BJ}^{2} + {CK}^{2} \right)= 3\left(a^{2} + b^{2} + c^{2}\right)\)
et
\({AI}^{2} + {BJ}^{2} + {CK}^{2} = \frac{3}{4} \left(a^{2} + b^{2} + c^{2} \right)\) ( 4 points )