Fonction Argument tangente hyperbolique de x
Définition :
L'application \(\textrm{th}\) : \(\mathbb{R} \to ]-1,1[\) continue et strictement croissante admet une fonction réciproque notée \(\textrm{Argth}\) : \(]-1,1[ \to \mathbb{R}\)
\(y = \textrm{Argth } x \Leftrightarrow x = \textrm{th }y\)
\(x \in ]-1,1[ \textrm{ et } y \in \mathbb{R}\)
\(\begin{array}{llr} \textrm{sh } (\textrm{Argth }x) = \frac{x}{\sqrt{1-x^{2}}} & \forall x \in ]-1,1[ \\ \textrm{ch } (\textrm{Argth }x) = \frac{1}{\sqrt{1-x^{2}}}& \forall x \in ]-1,1[ \\\textrm{th } (\textrm{Argth }x) = x \qquad& \forall x \in ]-1,1[ \\ \textrm{coth } (\textrm{Argth }x) = \frac{1}{x} \qquad& \forall x \in ]-1,0[ \cup]0,1[\end{array}\)
fonction impaire, d'où une étude sur \(D_{e} = [0, 1[\)
fonction dérivable sur \(D_{e}\) et :
\(\textrm{Argth'}x = \frac{1}{\textrm{th}'(\textrm{Argth }x)} = \frac{1}{1-\textrm{th}^{2}(\textrm{Argth }x)} = \frac{1}{1-x^{2}}>0\)
donc fonction croissante sur \(D_{e}\).
tableau de variation :

Représentation graphique de \(\textrm{Argth }x\)
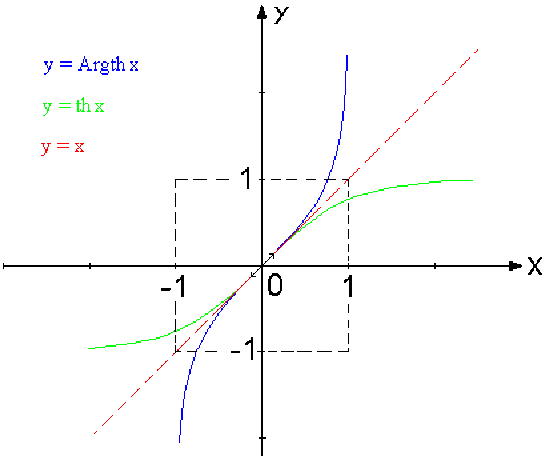
Expression logarithmique de \(\textrm{Argth }x\)
\(\forall x \in ]-1,1[ \qquad \textrm{Argth }x = \frac{1}{2} \ln \frac{1+x}{1-x}\)
Démonstration :
\(\forall (x, y) \in ]-1,1[ \times \mathbb{R},\)
\(y = \textrm{Argth }x \Leftrightarrow x = \textrm{th }y \Leftrightarrow x = \frac{e^{y} - e^{-y}}{e^{y} + e^{-y}} = \frac{e^{2y}-1}{e^{2y} + 1}\)
\(x\left(e^{2y}+1 \right) = e^{2y} - 1 \Leftrightarrow e^{2y} = \frac{1+x}{1-x}\)
\(y = \frac{1}{2} \ln \frac{1+x}{1-x}\)
On retrouve la fonction dérivée :
\(\left[\frac{1}{2}\ln\left(\frac{1+x}{1-x}\right)\right]' = \frac{1}{2} \left[\ln(1+x) - \ln(1-x)\right]' = \frac{1}{2}\left(\frac{1}{1+x} + \frac{1}{1-x}\right)\)
\(= \frac{1}{1-x^{2}} = \textrm{Argth}'x\)