Définition d'une fonction primitive
Définition : Fonction primitive
On appelle fonction primitive de la fonction d'une variable \(f(x),\) une fonction \(F(x)\) telle que : \(\color{red}F'(x) = f(x)\)
Exemple :
la fonction \(f(x) = 3x^2 - 4x + 5\) admet comme primitive \(F(x) = x^3 - 2x^2 + 5x\)
Deux primitives \(F(x)\) et \(G(x)\) d'une même fonction \(f(x)\) diffèrent d'une constante \(C.\) En effet :
\(F'(x) = G'(x) = f(x) \Leftrightarrow F'(x) - G'(x) = [F(x) - G(x)]' = 0\) d'où \(\color{red}F(x) - G(x) = C\)
Exemple :
\(F(x) = \cos^2x\) et \(G(x)=\frac{1}{2}\cos2x\)admettent pour fonction dérivée :
\(f(x) = F'(x) = G'(x) = - 2 \sin x \cos x\) d'où \(\color{red}F(x) - G(x) = C\)
Sachant que \(\cos^2x=\frac{1+\cos2x}{2}\Leftrightarrow\color{red}C=\frac{1}{2}\)
Interprétation géométrique
Soit la courbe \((C)\) d'équation \(y = f(x),\) les droites \(N_0M_0\) d'abscisse \(x_0\) fixe et \(NM\) d'abscisse \(x\) variable.
L'aire \(A = (N_0M_0MN)\) est une fonction de l'abscisse \(x.\)
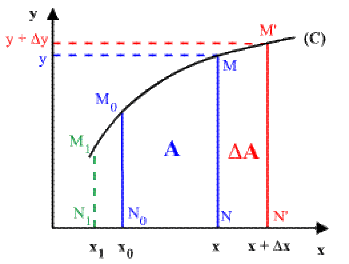
Posons : \(A = F(x)\) et montrons que cette aire \(F(x)\) est une fonction primitive de \(f(x)\) c.à.d. :
\(\boxed{\color{red}F'(x)=f(x)=\frac{dA}{dx}=\lim_{\Delta x\rightarrow 0}\frac{\Delta A}{\Delta x}}\)
Démonstration :
Posons : \(A= aire(N_0M_0MN) = F(x)\)
quand \(N(x) \rightarrow N'(x + \Delta x)\)
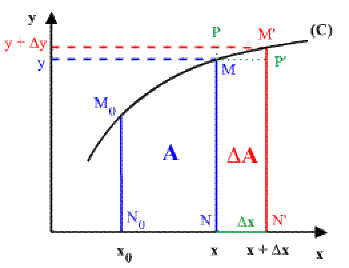
alors \(A(N_0M_0MN) \rightarrow A + \Delta A(N_0M_0M'N')\) avec \(\Delta A =( NMM'N')\)
or \(( NMP'N') <( NMM'N') <( NPM'N')\)
d'où \(y\Delta x < \Delta A < (y + \Delta y) \Delta x\)
et en divisant par \(\Delta x ^1 0\)
\(y < \Delta A / \Delta x < y + \Delta y\)
Comme \(\lim_{\Delta x\rightarrow 0}\frac{\Delta A}{\Delta x}=dF\Leftrightarrow\color{red}\frac{dA}{dx}=\frac{dF}{dx}=f(x)\)
La fonction primitive \(F(x)\) de la fonction \(f(x)\) est donc l'aire entre la courbe \((C),\) l'axe des abscisses et deux droites verticales d'abscisses \(x_0\) (fixe) et \(x\) (variable).
Remarque :
On aura toutes les fonctions primitives de \(f(x)\) en ajoutant une constante à \(A,\) c.à.d., en déplaçant \(N_0M_0\) en \(N_1M_1,\) l'aire \(A_1 = (N_1M_1MN) = G(x)\) ne diffère de
\(A = (N_0M_0MN)= F(x)\) que par l'aire fixe \((N_1M_1M_0N_0).\)
\(\color{red}G(x) = F(x) = \textrm{Constante}\)