Définition de l'intégrale indéfinie
Définition : Intégrale indéfinie
L'ensemble des primitives de \(f(x)\) est appelé intégrale indéfinie et l'on pose :
\(\boxed{\color{red}\int f(x)dx=F(x)+C}\)
Interprétation géométrique
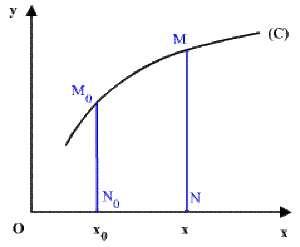
Soient les droites \(N_0M_0\) d'abscisse \(x_0\) fixe et \(NM\) d'abscisse \(x\) variable.
Si \(F(x)\) est une primitive quelconque de \(f(x)\) alors :
aire \((N_0M_0MN) = F(x) + C\)
Or d'après la définition de l'intégrale définie
aire\((N_0M_0MN)=\int_{x_0}^xf(x)dx\)
d'où :
\(\int_{x_0}^xf(x)dx=F(x)+C\)
La constante \(C\) dépendant de la borne inférieure \(x_0\) sera quelconque en ne mentionnant pas \(x_0.\) La limite supérieure étant toujours la variable \(x,\) celle-ci ne sera pas non plus indiquée, d'où
L'intégrale indéfinie : \(\boxed{\color{red}\int f(x)dx=F(x)+C}\)
Exemple :
\((3 x^2 + x - 1/x) dx = x^3 + x^2 / 2 - \ln |x| + C\)