Somme de trois tensions
Durée : 5 mn
Note maximale : 5
Question
Soient les trois tensions sinusoïdales de même pulsation : \(u_1(t)=2 . \cos(3t)\) ; \(\displaystyle{ u_2(t)=2 . \cos \left( 3t + \frac{\pi}{2} \right) }\) ; \(\displaystyle{ u_3(t) = 2 \sqrt{2} . \cos \left( 3t - \frac{\pi}{4} \right) }\)
Placer, dans le repère orthonormé \(xOy\), les vecteurs associés à \(u_1(t)\), \(u_2(t)\), \(u_3(t)\).
Faire la somme vectorielle \(\vec v = \vec v_1 + \vec v_2 + \vec v_3\).
Quelle est la norme de \(\vec v\) ?
Quel angle fait \(\vec v\) avec l'axe \(Ox\) ?
En déduire la tension sinusoïdale \(u(t)\) associée à \(\vec v\)
Solution
1.
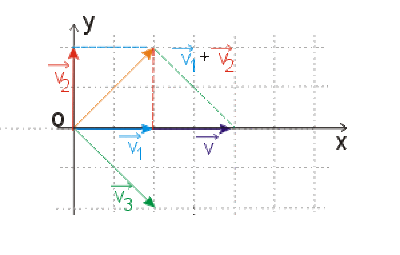
2.1. Norme de \(\vec v\) : 4
2.2. Angle que fait avec l'axe \(Ox\) : NUL
3. \(u(t) = 4 . \cos(3t)\) (5 pts)