Conducteurs ohmiques
Durée : 3 mn
Note maximale : 3
Question
\(R_1 = 100 \mathrm{ } \Omega\) ; \(R_2 = 1 \mathrm{ k} \Omega\) ; \(R_3 = 1 \mathrm{ k} \Omega\) ; \(\omega = 10^3 \mathrm{ rad/s}\).
En régime sinusoïdal permanent on peut écrire la relation : \(\underline{i} = G . \underline{u}\)
Donner l'expression de la conductance \(G\) du circuit.
Donner la relation qui relie la résistance totale du circuit à \(R_1\), \(R_2\) et \(R_3\).
Donner la valeur numérique de \(G\), en déduire celle de \(R\).
Solution
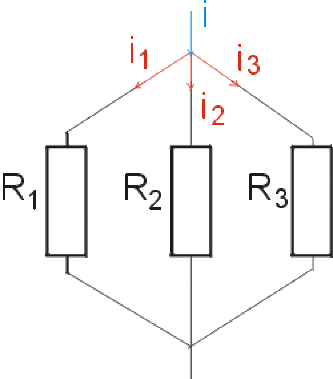
La loi des noeuds permet d'écrire : \(\underline{i} = \underline{i}_1 + \underline{i}_2 + \underline{i}_3\)
\(\displaystyle{ \underline{i} = \frac{\underline{u}}{R_1} + \frac{\underline{u}}{R_2} + \frac{\underline{u}}{R_3} }\)
donc \(\displaystyle{ G = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} = G_1 + G_2 + G_3 }\) (1 pt)
\(\displaystyle{ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} }\) (1 pt)
\(G = \mathrm{0,012 Siemens}\)
\(R \approx \mathrm{83,3 } \Omega\) (1 pt)