Dipôles en parallèle
Durée : 4 mn
Note maximale : 4
Question
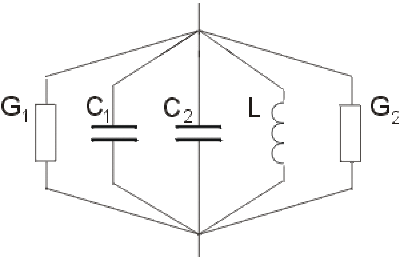
\(G_1 = \mathrm{0,02 s}\) ; \(G_2 = \mathrm{0,02 s}\) ; \(C_1 = 1 \mathrm{ \mu F}\) ; \(C_2 = 2 \mathrm{ \mu F}\) ; \(L = \mathrm{0,1 H}\) ; \(\omega = 10^3 \mathrm{ rad/s}\)
Donner l'expression de l'admittance complexe \(\underline{Y}\) de ce circuit sous la forme \(\underline{Y} = G + j . H\)
Quels noms portent respectivement \(G\) et \(H\) ?
Donner la valeur numérique de \(\underline{Y}\), en déduire celle de \(\underline{Z}\).
Le circuit équivalent est-il de type capacitif ou inductif ?
Solution
\(\displaystyle{ \underline{Y} = ( G_1 + G_2 ) + j . \left(C_1 . \omega + C_2 . \omega - \frac{1}{L . \omega} \right) = G + j . H }\) (1 pt)
\(G\) est la conductance, \(H\) est la susceptance. (1 pt)
\(\underline{Y} = 10^{-2} . (3 - j . \mathrm{0,7}) \mathrm{ Siemens}\)
\(\displaystyle{ \underline{Z} = 100 . \frac{1}{3 - j . \mathrm{0,7} } = 100.\frac{3 + j . \mathrm{0,7}}{ \mathrm{9,49} } }\)
d'où \(\underline{Z} \approx ( \mathrm{31,6} + j . \mathrm{7,38}) \mathrm{ } \Omega\) (1 pt)
Le circuit équivalent est inductif puisque la partie imaginaire de \(\underline{Z}\) est \(> 0\) (1 pt)