Antirésonance : Circuit bouchon
Définition :
Soit un dipôle dont la conductance varie avec la fréquence, alimenté par un générateur de courant délivrant une intensité constante. Si la conductance passe par un maximum, la tension aux bornes du dipôle sera alors maximale. A intensité constante à travers le dipôle, la tension passe par un maximum, ou, inversement, à tension constante aux bornes du dipôle, l'intensité passe par un minimum : ce phénomène est appelé antirésonance, et le circuit " bouchon " en est un exemple.
Circuit bouchon :
Ce circuit comprend trois dipôles en parallèle : un condensateur, une bobine, et un conducteur ohmique, supposés parfaits.
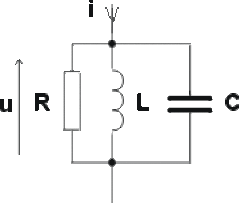
Les admittances complexes des trois branches ont pour expressions :
\(\displaystyle{\underline Y_1=\frac{1}{R} ;\;\underline Y_2=\frac{1}{jL\omega}}\)
\(\displaystyle{\underline Y_3 = jC\omega}\)
L'admittance complexe de l'ensemble est donnée par leur somme :
\(\displaystyle{\underline Y=\underline Y_1+\underline Y_2+\underline Y_3=\frac{1}{R}+\frac{1}{jL\omega}+jC\omega=\frac{1}{R}+j\big(C\omega-\frac{1}{L\omega}\big)=G+jH}\)
La conductance \(G\) et la susceptance \(H\) ont donc pour expression :
\(\displaystyle{G=\frac{1}{R} ;\;H=C\omega-\frac{1}{L\omega}}\)
le déphasage de la tension \(u(t)\) aux bornes du circuit par rapport à l'intensité \(i(t)\) du courant est :
\(\displaystyle{\varphi=-\textrm{Arctg}\frac{H}{G}=\textrm{Arctg}\frac{1-LC\omega^2}{RC\omega}}\)
et l'admittance du dipôle s'écrit :
\(\displaystyle{Y=\sqrt{\frac{1}{R^2}+\big(C\omega-\frac{1}{L\omega}\big)^2}}\)
Ce circuit est appelé "anti-résonnant" ou "bouchon" parce que, quand la relation
\(LC\omega^2 = 1\) est vérifiée, son admittance \(Y\) est minimale , ce qui signifie que l'intensité du courant total dans le diviseur de courant est minimale. Le courant et la tension sont alors en phase. Une application est l'élimination, dans un signal composite, d'une fréquence particulière. Dans le montage pratique, \(R\) représente alors la résistance de fuite du condensateur, qui est en général très grande, ce qui conduit à une faible valeur de \(Y\).