Oscillateur mécanique
Durée : 12 mn
Note maximale : 12
Question
On considère un oscillateur mécanique constitué d'une masse\(m\)attachée à l'extrémité d'un ressort horizontal, l'autre extrémité étant fixe.
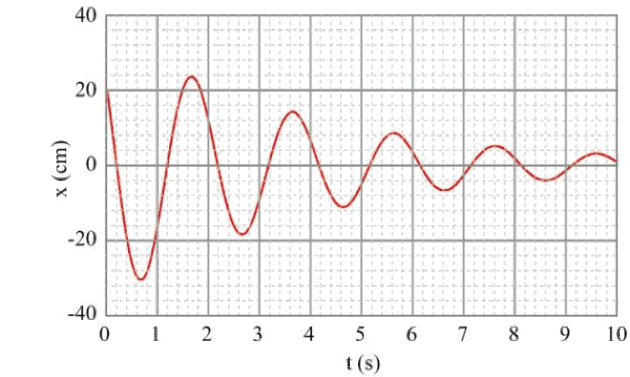
Le système est en oscillation et on mesure la position instantanée de la masse. Le graphe suivant décrit cette évolution.
Quel est le régime d'évolution de l'oscillateur ? Donner l'équation différentielle faisant intervenir le facteur d'amortissement et la pulsation propre à laquelle satisfait\(x(t)\). Donner l'expression générale de\(x(t)\). (3 pts)
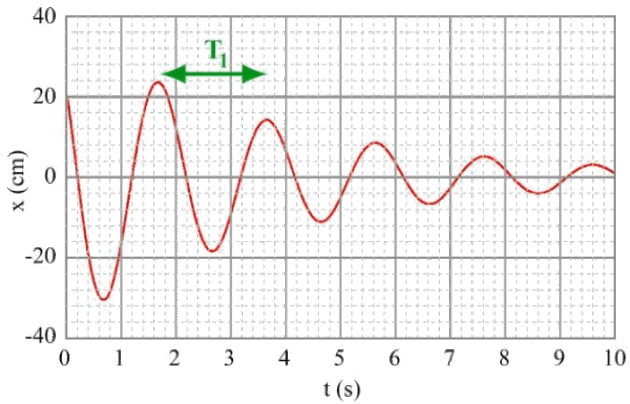
Déterminer graphiquement la pseudo-période d'oscillation que l'on notera\(T_{1}\). (2 pts)
Rappeler la définition du décrément logarithmique que l'on note\(\delta\). Déterminez-le graphiquement, puis exprimez-le littéralement en fonction du coefficient d'amortissement et de la pseudo-période. (4 pts)
Déduire les valeurs du coefficient d'amortissement, de la période propre et du facteur de qualité. (3 pts)
Solution
1. (3 pts) D'après le graphique, on constate que le régime d'évolution de l'oscillateur est un régime pseudo-périodique qui est régit par l'équation différentielle suivante :\(\frac{d^{2}x}{dt^{2}} + 2\lambda\frac{dx}{dt} + \omega_{0}^{2}x = 0\) \(\qquad\) où\(\lambda\)représente le coefficient d'amortissement et\(\omega_{0}\)la pulsation propre des oscillations.
L'expression générale de\(x(t)\)solution de cette équation est :\(\qquad\) \(x(t) = x_{m}e^{- \lambda t}\cos(\omega_{1}t + \varphi)\)
avec\(\omega_{1} = \sqrt{\omega_{0}^{2} - \lambda^{2}}\)représentant la pseudo-pulsation,\(\varphi\)la phase à l'origine et\(x_{m}\)une constante réelle.\(\varphi\)et\(x_{m}\)dépendent des conditions expérimentales.
2. (2 pts) La pseudo-période\(T_{1}\)est déterminée, par exemple, entre deux maxima du graphe :
Par la mesure, on trouve que\(T_{1} = 2\textrm{s}\).
3. (4 pts) Le décrément logarithmique\(\delta\)représente la décroissance de l'amplitude des oscillations. Il est défini comme le logarithme du rapport de deux extréma successifs de même signe de l'amplitude des oscillations :
\(\delta = \ln\frac{a(t_{n})}{a(t_{n} + T_{1})}\) \(\qquad\) où\(a(t_{n})\)et\(a(t_{n} + T_{1})\)représentent respectivement les amplitudes aux instant\(t_{n}\)et\(t_{n} + T_{1}\).
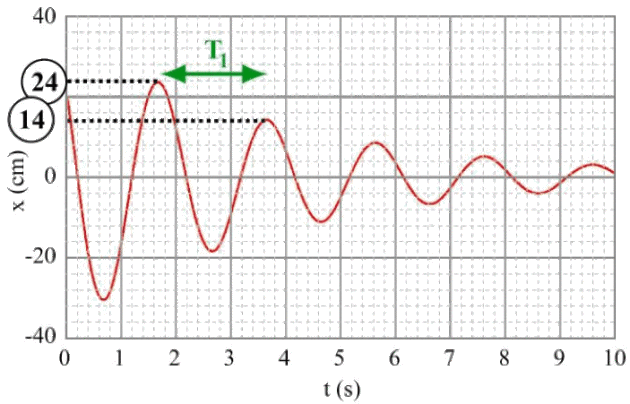
Graphiquement, on détermine le décrément logarithmique :
\(\delta = \ln\frac{24}{14}\)donc\(\delta = \mathrm{0,53}\).
On relie le décrément logarithmique à la pseudo-période et au coefficient d'amortissement en partant de la définition :
\(\delta = \ln\frac{a(t_{n})}{a(t_{n} + T_{1})} = \ln\bigg[\frac{x_{m}~\textrm{e}^{- \lambda t}\cos(\omega_{1}t + \varphi)}{x_{m}~\textrm{e}^{-\lambda(t + T_{1})}\cos(\omega_{1}(t + T_{1}) + \varphi)}\bigg]\)
Or, par définition, on a :\(\cos(\omega_{1}t + \varphi) = \cos(\omega_{1}(t + T_{1}) + \varphi)\)donc :\(\qquad\) \(\delta = \lambda T_{1}\)
4. (3 pts) Sachant que\(T_{1} = 2\textrm{s}\)et que\(\delta = \mathrm{0,53}\), on en déduit que :\(\qquad\) \(\lambda = \frac{\delta}{T_{1}} = \frac{\mathrm{0,53}}{2} = \mathrm{0,265}\textrm{s}^{-1}\)
De même, on a :
\(\omega_{1} = \sqrt{\omega_{0}^{2}-\lambda^{2}}\)donc :\(\frac{2\pi}{T_{1}} = \sqrt{\bigg(\frac{2\pi}{T_{0}}\bigg)^{2}-\lambda^{2}}\)où\(T_{0}\)représente la période propre des oscillations.
Donc\(T_{0} = \mathrm{1,99}\textrm{s}\).
Enfin, le facteur de qualité est défini comme suit :\(\qquad\) \(Q = \frac{\omega_{0}}{2\lambda} = \mathrm{5,96}\)