Oscillateur électrique
Durée : 10 mn
Note maximale : 10
Question
On considère un circuit électrique RLC représenté par la figure ci-dessous.
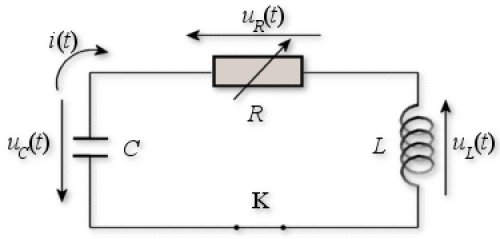
Il est composé de trois éléments montés en série : un condensateur\(C\), une bobine\(L\)de résistance interne négligeable et une résistance variable\(R\). On donne\(C = 10\mu\textrm{F}\)et\(L = 100\textrm{mH}\).
Le condensateur est initialement chargé. A l'instant\(t = 0\), on ferme l'interrupteur\(K\)et on laisse le système évoluer librement. On rappelle que la tension aux bornes du condensateur satisfait à l'équation différentielle :\(\frac{d^{2}u_{C}}{dt^{2}} + \frac{R}{L}\frac{du_{C}}{dt} + \frac{1}{LC}u_{C} = 0\).
On donne successivement à la valeur de la résistance 3 valeurs différentes :
\(R = 100~\Omega\)
\(R = 150~\Omega\)
\(R = 250~\Omega\)
1. Déterminer dans chacun des cas le régime de fonctionnement de cet oscillateur. Dans quel(s) cas observe-t-on des oscillations ? En déduire alors la pseudo-période. (3 pts)
2. Quelle valeur faut-il donner à\(R\)pour être en régime critique ? (2 pts)
On introduit maintenant en série un dipôle\(R'\)comportant un amplificateur opérationnel (\(n.b.\) : il n'est pas nécessaire de connaître le fonctionnement de ce type de composant pour répondre aux questions). Ce dipôle représente une « résistance négative » et permet d'apporter de l'énergie au système pour compenser les pertes par effet Joule.
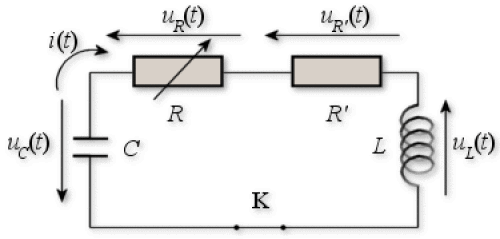
On montre alors que la tension aux bornes du condensateur satisfait à l'équation différentielle :\(\qquad\) \(\frac{d^{2}u_{C}}{dt^{2}} + \frac{R-R'}{L}\frac{du_{C}}{dt} + \frac{1}{LC}u_{C} = 0\)
La valeur de\(R'\)est fixée égale à\(R\).
3. Quel est le régime de fonctionnement de cet oscillateur ? (1 pt). En déduire l'expression littérale de la tension\(u_{C}(t)\), solution de l'équation différentielle. (2 pts)
4. Donner l'expression numérique de la tension\(u_{C}(t)\)en considérant qu'à\(t = 0\), la tension aux bornes du condensateur est maximale et égale à \(\textrm{6 V}.\) (2 pts)
Solution
(3 pts) L'équation différentielle qui décrit la tension aux bornes du condensateur est de la forme :\(\qquad\) \(\frac{d^{2}u_{C}}{dt^{2}} + 2\lambda\frac{du_{C}}{dt} + \omega_{0}^{2}u_{C} = 0\)
avec\(\lambda = \frac{R}{2L}\)et\(\omega_{0} = \frac{1}{\sqrt{LC}}\).
C'est la comparaison de\(\lambda\)avec\(\omega_{0}\)qui permettra de déterminer le régime de fonctionnement de l'oscillateur.
Dans les 3 cas, la valeur de\(\omega_{0}\)reste identique et égale à\(\omega_{0} = 1000\textrm{rad.s}^{-1}\). En revanche, la valeur du coefficient d'amortissement dépend de la valeur de la résistance, nous envisageons donc les 3 cas :
1er cas :\(R = 100~\Omega \Rightarrow \lambda = 500\textrm{s}^{-1}\)
\(\lambda<\omega_{0}\), on est donc dans un régime pseudo-périodique. Les oscillations ont une pseudo-période\(T_{1}\)égale à :\(T_{1} = \frac{2\pi}{\sqrt{\omega_{0}^{2} - \lambda^{2}}} = \mathrm{7,26}\textrm{ms}\)
2e cas :\(R = 150~\Omega \Rightarrow \lambda = 750\textrm{s}^{-1}\)
\(\lambda<\omega_{0}\), on est donc dans un régime pseudo-périodique. Les oscillations ont une pseudo-période\(T_{1}\)égale à :\(T_{1} = \frac{2\pi}{\sqrt{\omega_{0}^{2} - \lambda^{2}}} = \mathrm{9,50}\textrm{ms}\)
3e cas :\(R = 250~\Omega \Rightarrow \lambda = 1250\textrm{s}^{-1}\)
\(\lambda>\omega_{0}\), on est donc dans un régime apériodique et il n'y a pas d'oscillation.
(2 pts) Le régime critique est défini lorsque\(\lambda = \omega_{0}\). Il suffit donc de remplacer\(\lambda\)et\(\omega_{0}\)par leurs expressions littérales :
\(\lambda = \frac{R}{2L} = \omega_{0} = \frac{1}{\sqrt{LC}} \Leftrightarrow R = 2\sqrt{\frac{L}{C}}\)
A.N. :\(R = 2\sqrt{\frac{\mathrm{0,1}}{10.10^{-6}}} = 200~\Omega\)
(1 pt) Si\(R = R'\), alors le coefficient d'amortissement s'annule :\(\lambda = 0\). Le système se comporte alors comme un oscillateur harmonique non amorti.
(2 pts) L'équation différentielle se simplifie donc et devient :
\(\frac{d^{2}u_{C}}{dt^{2}} + \omega_{0}^{2}u_{C} = 0\)avec\(\omega_{0}^{2} = \frac{1}{LC}\)
La solution à cette équation est de la forme :\(u_{C} = u_{Cm}\cos(\omega_{0}t + \varphi)\)
où l'amplitude\(u_{Cm}\)et la phase à l'origine\(\varphi\)sont deux constantes réelles qui dépendent des conditions initiales.\(\omega_{0}\)est la pulsation propre de l'oscillateur.
(2 pts) L'expression numérique de la tension aux bornes du condensateur se calcule à partir des conditions initiales : à\(t = 0\),\(u_{C} = 6\textrm{V}\)donc\(u_{Cm}\cos(\varphi) = 6\). De plus, on sait qu'à\(t = 0\),\(u_{C}\)est maximale donc\(\cos(\varphi) = 1\)soit\(\varphi = 0\). On en conclut :
\(\displaystyle{ \left[\begin{array}{ll} \varphi = 0 \\ u_{Cm} = 6\end{array}\right.}\)
Enfin, la valeur de\(\omega_{0}\)est égale à\(\frac{1}{\sqrt{LC}}\) , soit\(\omega_{0} = 1000\textrm{rad.s}^{-1}\).
On obtient finalement\(u_{C}(t) = 6\cos(1000t)\), exprimée en volts.