L'oscillateur harmonique forcé : présentation
Le système physique de type « oscillateur harmonique amorti » (dont l'étude, objet d'une autre ressource, est considérée comme acquise) est soumis à une excitation permanente, décrite par la fonction \(f(t)\) et produite par un dispositif extérieur appelé excitateur.
L'excitateur fournit à tout instant de l'énergie au système.
Dans ce cas la grandeur \(q(t)\) décrivant l'évolution du système au cours du temps satisfait à l'équation différentielle avec second membre :
\(q"(t) + 2 ~\lambda~ q'(t) + \omega_0^2 ~q(t) = h(t)\)
Le système est appelé oscillateur forcé. La solution \(q(t)\) de l'équation (ou réponse de l'oscillateur) décrit les oscillations forcées du système. L'oscillateur évolue suivant un régime transitoire forcé du second ordre puis suivant un régime permanent.
Si \(\lambda = 0\), l'oscillateur est dit sans amortissement.
Rappelons que la pulsation propre \(\omega_0\) et le coefficient d'amortissement \(\lambda\) s'expriment en \(\mathrm{ rad.s}^{-1}\), \(q\) et \(h\) s'expriment en unité \(\mathrm{SI}\) des grandeurs physiques représentées.
L'équation ci-dessus est une équation différentielle du second ordre, à coefficients constants, avec un second membre noté \(h(t)\).
Le second membre \(h(t)\) diffère de l'excitation \(f(t)\). \(h(t)\) s'exprime simplement en fonction de \(f(t)\) (multiplication par une constante, déphasage), des exemples sont étudiés par la suite, son expression dépend :
du type de système excité : électrique, mécanique, acoustique, moléculaire, atomique...
du type de l'excitation : électrique, mécanique (en force, en déplacement), excitation par de la lumière...
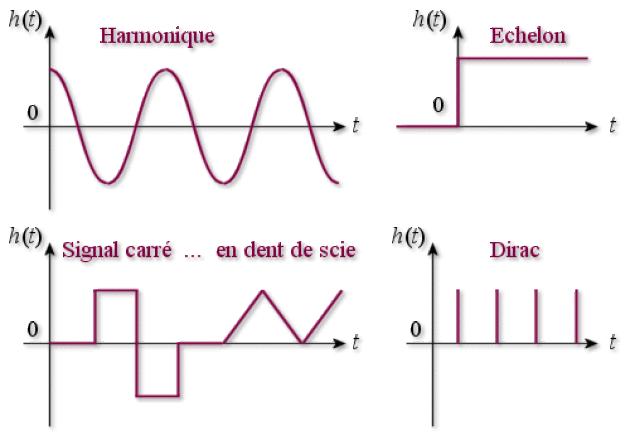
de la forme de l'excitation : sinusoïdale, en échelon, en impulsions rectangulaires, en dents de scie, en impulsions de Dirac...
Les principales excitations \(h(t)\) sont représentées dans la figure ci-dessous :