Oscillateur harmonique forcé, oscillations forcées

Le circuit série (R, L, C), soumis à l'excitation \(u(t) = U_m ~\cos ~\Omega t\), est décrit dans l'exemple précédent.

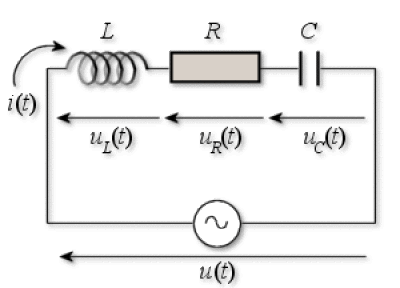
Rappelons les équations en intensité et en tension établies :

\(i"(t) + \frac{R}{L} i'(t) + \frac{1}{LC} i(t) = - \frac{\Omega U_m}{L} \sin ~\Omega t = \frac{\Omega U_m}{L} \cos \bigg(\Omega t + \frac{\pi }{2}\bigg)\)

\(u_c^"(t) + \frac{R}{L}u'_c(t) + \frac{1}{LC}~ u_c(t) = \frac{U_m}{LC} \cos ~\Omega t\)

La résolution de ces deux équations différentielles en régime permanent sinusoïdal se fait en utilisant la méthode de la représentation complexe développée dans le cas de l'oscillateur mécanique.

L'étude de la résonance d'amplitude correspond à l'étude de la d.d.p., \(u_c(t)\), aux bornes du condensateur en fonction de la pulsation d'excitation \(\Omega\).

Ces calculs sont effectués dans les exercices de la ressource sur les oscillations forcées où sont étudiés :

• Circuit série (R, L, C) et intensité en régime permanent sinusoïdal.

• Circuit série (R, L, C) et d.d.p. aux bornes du condensateur en régime permanent sinusoïdal.

• Circuit série (R, L, C) et résonance en tension aux bornes du condensateur.