Equation différentielle associée à l'oscillateur
Partie
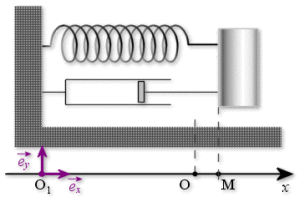
On considère le système amorti, constitué d'une masse \(m\) se déplaçant horizontalement sans frottement sur un plan fixe, d'un ressort de raideur \(k\) et d'un amortisseur de coefficient visqueux \(\mu\).
On applique subitement à la masse \(m\) une force constante \(\vec{F}_{exc} = F_{0}\vec{e}_{x}\),\(F_{0}\) étant une constante positive. La masse est assimilée à un point matériel en \(M\), le référentiel \((O,\vec{e}_{x}, \vec{e}_{y})\) est galiléen.
On désigne par \(x(t)\) l'abscisse de \(M\) repérée par rapport à sa position initiale d'équilibre \(O\),\(x(t) = \overline{OM}(t)\).
Question
Quelles sont les caractéristiques de l'excitation appliquée au système ?
Solution détaillée
Il s'agit ici d'une excitation en force. L'intensité \(F_{0}\) de la force est constante, l'excitation est donc uniforme. Enfin la force est constamment dirigée dans le sens positif de l'axe \(O\vec{e}_{x}\). Le graphe de l'excitation en fonction du temps a la forme d'un échelon.
Question
Etablir le bilan des forces appliquées à la masse en mouvement.
Ecrire le principe fondamental de la dynamique relatif à \(m\) et montrer que \(x(t)\) satisfait à l'équation différentielle :
\(x'' + 2\lambda x' + \omega_{0}^{2} x = \frac{F_{0}}{m}\)
avec \(\lambda = \frac{\mu}{2m}\) (coefficient d'amortissement de l'oscillateur) et \(\omega_ {0} = \sqrt{\frac{k}{m}}\) (pulsation propre).
Solution détaillée
Les forces appliquées sont : le poids \(\vec{P}\), la force de réaction du support \(\vec{R}_{n}\)(normale à celui-ci), la force de rappel du ressort \(\vec{F}_{r}\), la force d'amortissement visqueux \(\vec{F}_{d}\) et la force d'excitation \(\vec{F}_{exc}\).
Le repère de l'observateur étant supposé galiléen, le P.F.D. appliqué à \(m\) à un instant \(t\), s'écrit :
\(\vec{P} + \vec{R}_{n} + \vec{F}_{r} + \vec{F}_{d} + \vec{F}_{exc} = m \vec{\gamma}\)
Les différents termes s'expriment en fonction de la base vectorielle \(\vec{e}_{x} ,\vec{e}_{y}\):
\(\vec{P} = -mg \vec{e}_{y}\), \(\vec{R}_{n} = R \vec{e}_{y}\), \(\vec{F}_{r} = -kx \vec{e}_{x}\), \(\vec{F}_{r} = - kx \vec{e}_{x}\), \(\vec{F}_{d} = - \mu x' ~\vec{e}_{x}\) et \(\vec{F}_{exc} = F_{0} \vec{e}_{x}\);
le mouvement étant horizontal, \(\vec{\gamma} = \gamma \vec{e}_{x} = x'' \vec{e}_{x}\).
Par projection sur la direction verticale (c'est-à-dire en faisant le produit scalaire des deux membres de l'équation vectorielle par \(\vec{e}_{y}\)), on obtient la relation scalaire : \(-mg + R = 0\)
Par projection sur la direction horizontale : \(- kx - \mu x' + F_{0} = m x''\)
Soit, en ordonnant les termes : \(x'' + 2 \lambda x' + \omega_{0}^{2} x = \frac{F_{0}}{m}\)
Question
Sachant que \(m =\textrm{1 kg},\) \(k = \textrm{1 N.m}^{-1},\) \(\mu = \textrm{0,5 N.s.m}^{-1}\) et \(F_{0} = \textrm{0,1 N},\)calculer \(\lambda\) et \(\omega_{0}\) et \(\frac{F_{0}}{m}\), en déduire l'expression numérique de l'équation différentielle :
\(x'' + \mathrm{0,5} x' + x = \mathrm{0,1}\)
dans laquelle tous les termes sont exprimés en unités S.I.
Solution détaillée
Valeurs numériques :
\(\lambda = \frac{\mu}{2m} = \frac{\mathrm{0,5}}{2 \times 1} = \textrm{0,25 s}^{-1}\) et \(\omega_{0} = \sqrt{\frac{k}{m}} = \sqrt{\frac{1}{1}} = \textrm{1 rad.s}^{-1}\),
\(\frac{F_{0}}{m} = \frac{\mathrm{0,1}}{1} = \textrm{0,1 ms}^{-2}\).
On en déduit \(x'' + \mathrm{0,5} x' + x = \mathrm{0,1}\), équation exprimée en unités S.I.
Question
Ecrire les conditions initiales du problème.
Solution détaillée
Les deux conditions initiales du problème s'écrivent :
\(x(t=0)=0 ~~~\) \(\qquad\) \(\qquad\) \(M\) est en \(O\) à l'instant \(t = 0\),
\(\dot{x}(t=0)=0 ~~~\) \(\qquad\) \(\qquad\) on applique la force sur une masse initialement immobile.
\(\qquad\)
Remarque : Unités
Dans le système international d'unités, la pulsation s'exprime en \(\textrm{rad.s}^{-1}\) et la phase à l'origine des temps doit être exprimée en radian de telle sorte que la quantité \(\omega t + \varphi\) soit sans dimension (on rappelle que s'il existe différentes unités pour exprimer les angles, cette mesure peut toujours se ramener à un rapport de longueur).