Résonance d'amplitude, oscillateur mécanique amorti et forcé
Partie
On considère un système oscillant amorti et forcé du même type que celui étudié dans le test précédent. L'expression de la force d'excitation harmonique, de pulsation \(\Omega\), appliquée à la masse \(m\) s'écrit \(\vec{F}_{exc}(t) = F_{m} \cos \Omega t \vec{e}_{x}\).
On étudie les oscillations en régime permanent. On rappelle que dans ce cas l'expression de l'abscisse \(x(t)\) de la masse \(m\), repérée par rapport à sa position d'équilibre, est
\(x(t) \approx x_{pm} \cos(\Omega t + \Phi_{p})\) où \(x_{pm}\) désigne l'amplitude des oscillations.
On se propose d'étudier la variation de \(x_{pm}\) lorsque la pulsation \(\Omega\) de la force d'excitation varie de la valeur \(\Omega = 0\) à la valeur \(\Omega \to + \infty\).
En régime permanent :
Dans le cas d'un oscillateur mécanique amorti, soumis à une force d'excitation harmonique d'amplitude \(F_{m}\) et de pulsation \(\Omega\), l'amplitude des oscillations \(x_{pm}\), s'exprime en fonction des données par la relation \(x_{pm} (\Omega ) = \frac{F_{m}/m}{\sqrt{(\omega_{0}^{2} - \Omega^{2})^{2} + (2 \lambda \Omega)^{2}}}\)
Si l'oscillateur est tel que \(\lambda < \frac{\omega_{0}}{\sqrt{2}}\): l'amplitude des oscillations, lorsque \(\Omega\) varie, passe par un maximum pour la valeur particulière \(\Omega_{r}\) de \(\Omega\), appelée pulsation de résonance, telle que : \(\Omega_{r} = \sqrt{\omega_{0}^{2} - 2 \lambda^{2}}\). Le graphe de la fonction \(x_{pm}(\Omega)\) présente un pic de résonance. Ce pic est d'autant plus marqué que le coefficient d'amortissement \(\lambda\) est faible par rapport à la pulsation propre \(\omega_{0}\).
Si l'oscillateur est tel que \(\lambda \ge \frac{\omega_{0}}{\sqrt{2}}\): le maximum de l'amplitude des oscillations a lieu pour la valeur \(\Omega = 0\) et il n'y a pas de pic de résonance.
Question
Déterminer la valeur de la pulsation de résonance \(\Omega_{r}\) et discuter l'existence de la résonance d'amplitude.
Solution détaillée
La fonction \(x_{pm} (\Omega ) = \frac{F_{m}/m}{\sqrt{(\omega_{0}^{2} - \Omega^{2})^{2} + (2 \lambda \Omega)^{2}}}\) est strictement positive.
L'étude de cette fonction montre qu'elle présente dans tous les cas un maximum.
Posons : \(x_{pm} = \frac{F_{m}/m}{\sqrt{D}}\) avec \(D = (\omega_{0}^{2} - \Omega^{2})^{2} + (2 \lambda \Omega)^{2}\) . Les valeurs de \(\Omega\) correspondantes se déterminent en annulant la dérivée première du dénominateur ou de la quantité sous le radical par rapport à \(\Omega\), soit :
\(\frac{\textrm{d } D(\Omega)}{\textrm{d } \Omega} = 2( \omega_{0}^{2} - \Omega^{2})(-2 \Omega) + 8 \lambda^{2} \Omega = 4 \Omega ( \Omega^{2} + 2 \lambda^{2} - \omega_{0}^{2}) = 0\)
On constate que cette expression s'annule :
soit pour \(\Omega = 0\),
soit pour \(\Omega^{2} + 2 \lambda^{2} - \omega_{0}^{2} = 0\) ou \(\Omega = \Omega_{r} = \sqrt{\omega_{0}^{2} - 2 \lambda^{2}}\). Cette dernière valeur est appelée pulsation de résonance.
Le résultat précédent montre que \(\Omega_{r}\) est définie si \(\omega_{0}^{2} - 2 \lambda^{2} >0\), soit si \(\lambda < \frac{\omega_{0}}{\sqrt{2}}\) (ou en introduisant les expressions \(\lambda = \frac{\mu}{2m}\) et \(\omega_{0} = \sqrt{\frac{k}{m}}\): \(\mu < \sqrt{2mk}\)). Dans ce cas le graphe de la fonction \(x_{pm}(\Omega)\) présente un pic de résonance.
Si \(\lambda \ge \frac {\omega_{0}}{\sqrt{2}}\) (ou \(\mu \ge \sqrt{2mk}\), le maximum se produit pour \(\Omega = 0\), l'amplitude des oscillations \(x_{pm}\) décroit lorsque \(\Omega\) augmente. Il n'y a pas de pic de résonance.
Question
Calculer les valeurs respectives de \(x_{pm}\) pour \(\Omega = 0\), \(\Omega \to + \infty\) et \(\Omega = \Omega_{r}\).
Solution détaillée
A partir de l'expression de \(x_{pm}( \Omega)\) on obtient les trois expressions de l'amplitude correspondantes aux valeurs \(0\), \(+\infty\) et \(\Omega_{r}\) de la pulsation :
\(x_{pm}(\Omega = 0) = \frac{F_{m}/m}{\omega_{0}^{2}}\) \(\qquad\) \(x_{pm} ( \Omega \to + \infty ) \to 0\) par valeur positive
et en tenant compte de \(\Omega_{r}^{2} = \omega_{0}^{2} - 2 \lambda^{2}\).
\(x_{pm}(\Omega = \Omega_{r}) = \frac{F_{m}/m}{\sqrt{\big[\omega_{0}^{2} - (\omega_{0}^{2} - 2 \lambda^{2}) \big]^{2} + 4 \lambda^{2}( \omega_{0}^{2} - 2 \lambda^{2})}} = \frac{F_{m}/m}{2 \lambda \sqrt{\omega_{0}^{2} - \lambda^{2}}}\)
Question
Calculer le rapport \(R = \frac{x_{pm} ( \Omega = \Omega_{r})}{x_{pm}(\Omega = 0)}\) et exprimer \(R\) en fonction du facteur de qualité \(Q = \frac{\lambda}{\omega_{0}}\).
Solution détaillée
A partir des résultats précédents, le rapport \(R\) s'écrit :
\(R = \frac{\omega_{0}^{2}}{2 \lambda \sqrt{\omega_{0}^{2} - \lambda^{2}}} = \frac{\omega_{0}}{2 \lambda} \frac{1}{ \sqrt{1 - \frac{\lambda^{2}}{\omega_{0}^{2}}}} = Q \frac{1}{\sqrt{1 - \frac{1}{4 Q^{2}}}}\)
Question
Application numérique :
On donne : \(m = \textrm{0,1 kg}\) ; \(k = \textrm{ 3,6 N.m}^{-1}\) ; \(F_{m} = \textrm{0,1 N}\).
On étudie l'oscillateur pour deux amortissements différents, correspondant successivement aux deux valeurs numériques \(\mu_{1} = \textrm{0,6 Nm}^{-1}\textrm{s}\) et \(\mu_{2} = \textrm{0,06 Nm}^{-1}\textrm{s}\) du coefficient relatif à la force d'amortissement visqueux.
Calculer dans les deux cas, les valeurs numériques de \(\omega_{0}\),\(\lambda\), \(\Omega_{r}\), \(x_{pm}(\Omega = 0)\) , \(x_{pm}(\Omega = \Omega_{r})\) , \(R\) et du facteur de qualité \(Q\).
Présenter ces résultats dans un tableau formé de deux lignes relatives à \(\mu_{1}\) et \(\mu_{2}\).
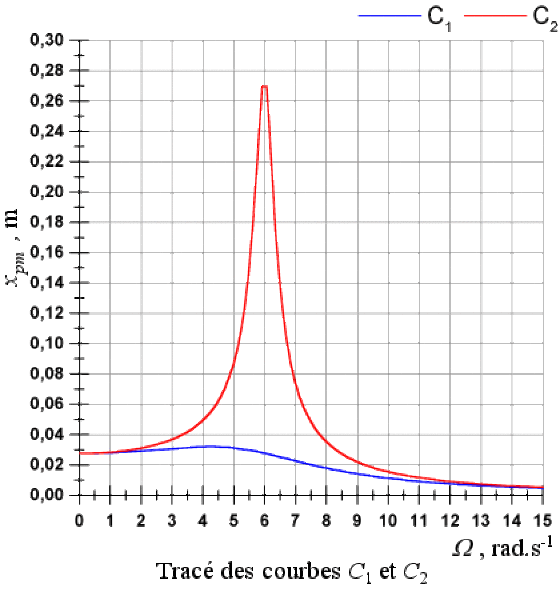
Tracer les graphes \(C_{1}\) et \(C_{2}\) de la fonction \(x_{pm}(\Omega)\), relatifs respectivement à \(\mu_{1}\) et \(\mu_{2}\). Choisir pour cela les échelles suivantes : \(\textrm{1 rad s}^{-1}\) pour \(\textrm{1 cm}\), de \(0\) à \(\textrm{14 rad s}^{-1}\) en abscisse et \(\textrm{0,02 m}\) pour \(\textrm{1 cm}\), de \(0\) à \(\textrm{0,30 m}\) en ordonnée.
Commenter les résultats obtenus.

Solution détaillée
Application numérique :
Sachant que \(m = \textrm{0,1 kg}\); \(k = \textrm{3,6 N.m}^{-1}\); \(F_{m} = \textrm{0,1 N}\), il vient :
\(\mu\)
\(\omega_{0}\)
\(\lambda\)
\(\Omega_{r}\)
\(x_{pm}(0)\)
\(x_{pm}(\Omega_{r})\)
\(R\)
\(Q\)
\(\mu_{1} = \mathrm{0,6}\)
6
3
4,24
28
32
1,14
1
\(\mu_{2} = \mathrm{0,06}\)
6
0,3
5,98
28
278
9,93
10
\(\textrm{N m}^{-1}\textrm{s}\)
\(\textrm{rad s}^{-1}\)
\(\textrm{rad s}^{-1}\)
\(\textrm{rad s}^{-1}\)
\(\textrm{mm}\)
\(\textrm{mm}\)
\(\textrm{mm}\)
\(\textrm{mm}\)
Les graphes \(C_{1}\) et \(C_{2}\) de la fonction \(x_{pm}(\Omega)\), correspondant respectivement aux valeurs \(\mu_{1}\) et \(\mu_{2}\), sont représentés dans la figure ci-dessous.
Commentaires :
Les deux courbes présentent un pic de résonance (la condition \(\lambda < \frac{\omega_{0}}{\sqrt{2}}\) est vérifiée dans les deux cas).
Le pic de résonance relatif à la courbe \(C_{1}\) est très aplati, le facteur de qualité est faible \((Q = 1)\). Au contraire la courbe \(C_{2}\) présente un pic de résonance marqué, le facteur de qualité est plus élevé \((Q = 10)\). Remarquons que la courbe \(C_{2}\) correspond à l'amortissement le plus faible.
On constate que le sommet des deux courbes se décale vers la droite lorsque l'amortissement diminue : \(\Omega_{r}~(C_{1}) = \mathrm{4,24} < \Omega_{r} ~(C_{2}) = \mathrm{5,98} \approx \omega_{0} = 6 ~\big( \textrm{rad s}^{-1}\big)\).