Ondes planes monochromatiques
(champs électriques incident, réfléchi, transmis)
L'onde réfléchie et l'onde transmise (réfractée) par le dioptre séparant les deux milieux étant planes et harmoniques (comme l'onde incidente), on ne sait pas encore si la pulsation de ces trois ondes est la même.
En notant \(V_1\) et \(V_2\) les vitesses respectives des ondes dans les milieux \((1)\) et \((2)\) , on aura :
\(\vec K_i = \vec u_i . K_i \textrm{ avec } K_i = \frac{\omega_i}{V_1},\quad \vec K_r = \vec u_r . K_r \textrm{ avec } K_r = \frac{\omega_r}{V_1}, \quad \vec K_t = \vec u_t . K_t \textrm{ avec } K_t = \frac{\omega_t}{V_2}\)
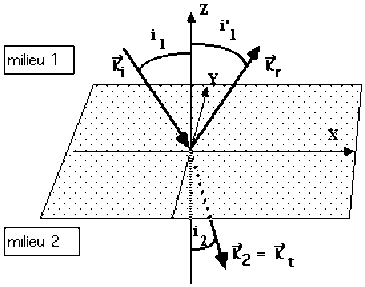
On admettra que l'on peut approximer la surface de séparation des milieux \((1)\) et \((2)\), au point considéré, par le plan tangent en ce point. La normale à ce plan sera prise avec pour direction \(OZ\).
L'intersection du plan \(( OZ , \vec K_i )\) avec le plan séparant les deux milieux définit la direction \(OX\).
En notation complexe, les ondes (planes, monochromatiques) incidente, réfléchie et transmise s'expriment respectivement :
\(\vec E_i = \vec E_{i0} ~.~ \exp j[\omega_i t - \vec K_i . \vec r] = \vec E_{i0} ~.~ \exp j[\omega_i t - K_i (\alpha_i . x + \gamma_i . z)] ~~~ \textrm{ avec } \beta_i = 0 ~ \textrm{ et } \alpha_i = \sin i_1\)
\(\vec E_r = \vec E_{r0} ~.~ \exp j[\omega_r t - \vec K_r . \vec r + \phi_r] = \vec E_{r0} ~.~ \exp j[\omega_r t - K_r (\alpha_r . x + \beta_r . y + \gamma_r . z) + \phi_r]\)
\(\vec E_t = \vec E_{t0} ~.~ \exp j[\omega_t t - \vec K_t . \vec r + \phi_t] = \vec E_{t0} ~.~ \exp j[\omega_t t - K_t (\alpha_t . x + \beta_t . y + \gamma_t . z) + \phi_t]\)
Remarque :
On note : \(\alpha_i\), \(\alpha_r\), \(\alpha_t\) les cosinus directeurs respectifs des directions incidente, réfléchie et transmise.
Remarquer que \(\alpha_i = \cos (\vec K_i, \vec x) = \cos \Big( \frac{\pi}{2} - i_1\Big) = \sin i_1\) et que l'on aura la même relation pour les cosinus directeurs \(\alpha_r\) et \(\alpha_t\) des directions réfléchie et transmise quand on aura montré que \(\vec K_r\) et \(\vec K_t\) sont aussi dans le plan d'incidence.
On note : \(\phi_r\) et \(\phi_t\) les déphasages possibles, par rapport à l'onde incidente \(\vec E_i\), produits respectivement par les phénomènes de réflexion et de transmission.
Compte tenu que les relations de continuité, pour le champ électrique, s'expriment par l'égalité des composantes tangentielles, il convient maintenant de déterminer les composantes tangentielles de chacun de ces champs (incident, réfléchi et transmis) pour pouvoir ensuite appliquer ces relations de continuité.